طباعة الدرس

أتحقق من فهمي

القيم القصوى والتقعر

القيم القصوى المحلية والمطلقة

أتحقق من فهمي صفحة 96

أجد القيم القصوى المحلية والقيم القصوى المطلقة (إن وجدت) للاقتران المعطى تمثيله البياني في كلّ ممّا يأتي:

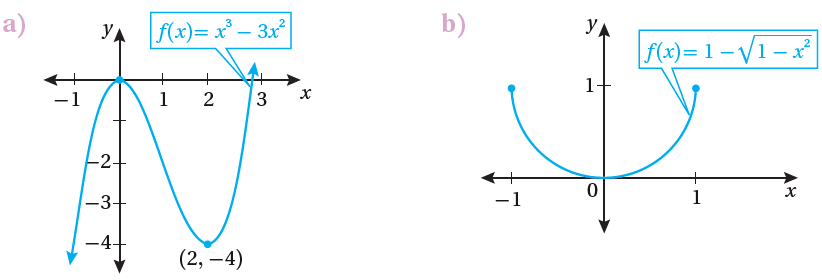
(a) ليس للاقتران f قيم قصوى مطلقة.

للاقتران قيمة عظمى محلية عند x = 0 هي f (0) = 0

وله قيمة صغرى محلية عند x = 2 هي f (2) = -4  

(b) للاقتران قيمة عظمى مطلقة عند x = 1 و x = -1 هي f ($\pm$1) = 1

وله قيمة صغرى محلية ومطلقة عند x = 0 هي f (0) = 0  

---

القيم القصوى المطلقة على الفترات المغلقة

أتحقق من فهمي صفحة 102

أجد القيمة العظمى المطلقة والقيمة الصغرى المطلقة (إن وجدت) لكلّ اقتران ممّا يأتي في الفترة المعطاة:

(a) $f\left(x\right)=x^3-6x^2+5,[-3,5]$

$\begin{array}{rl}& f\left(x\right)=x^3-6x^2+5,[-3,5]\\ & f^{\mathrm{\prime }}\left(x\right)=3x^2-12x=0\to 3x(x-4)=0\to x=0, x=4\end{array}$

نقارن قيم الاقتران عند النقط الحرجة وعند طرفي مجاله.

وتكون قيم x الحرجة هي: x = 0 , x = 4

$\begin{array}{rl}& f(-3)=-27-54+5=-76, f\left(0\right)=5\\ & f\left(4\right)=64-96+5=-27, f\left(5\right)=125-150+5=-20\end{array}$

للاقتران قيمة صغرى مطلقة عند x = -3 هي f (-3) = -76

وله قيمة عظمى محلية ومطلقة عند x = 0 هي f (0) = 5  

(b) $f\left(x\right)=\sqrt[3]{x}, [-8,8]$

$\begin{array}{rl}& f\left(x\right)=x^{\frac{1}{3}},[-8,8]\\ & f^{\mathrm{\prime }}\left(x\right)=\frac{1}{3}{x}^{-\frac{2}{3}}=\frac{1}{3\sqrt[3]{x^2}}\end{array}$

f ’(x) لا تساوي صفراً لأي قيمة في (-8, 8)، وهي غير موجودة عند x = 0 وهذه هي القيمة الحرجة فقط.

$\begin{array}{rl}& f(-8)=-2\\ & f\left(0\right)=0\\ & f\left(8\right)=2\end{array}$

للاقتران قيمة صغرى مطلقة عند x = -8 هي f (-8) = -2

وله قيمة عظمى محلية ومطلقة عند x = 2 هي f (8) = 2  

(c) $f\left(x\right)={\sin }^2 x+\cos x,[0, 2\pi ]$

أجد القيم الحرجة في الفترة (0, 2π)

$\begin{array}{rl}{f}^{\mathrm{\prime }}\left(x\right)=2sin x cos x-sin x=0& \to sin x(2cos x-1)=0\\ & \to sin x=0 \text{or }cos x=\frac{1}{2}\\ & \to x=\pi , \text{or }x=\frac{\pi }{3}, x=\frac{5\pi }{3}\end{array}$

وتكون قيم  الحرجة هي: $x=\pi , x=\frac{\pi }{3}, x=\frac{5\pi }{3}$

أجد قيم الاقتران عند القيم الحرجة وطرفي مجاله.

$\begin{array}{rl}& f\left(0\right)=1\\ & f\left(\frac{\pi }{3}\right)=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}\\ & f\left(\pi \right)=-1\\ & f\left(\frac{5\pi }{3}\right)=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}\\ & f\left(2\pi \right)=1\end{array}$

للاقتران قيمة صغرى محلية ومطلقة عند x = π هي f (π) = -1

وله قيمة عظمى محلية ومطلقة عند $x=\frac{\pi }{3}, x=\frac{5\pi }{3}$ هي $\frac{5}{4}$

---

إيجاد القيم القصوى المحلية

أتحقق من فهمي صفحة 105

أجد القيم القصوى المحلية (إن وجدت) للاقتران:

$\begin{array}{rl}& f\left(x\right)=(x-1)e^x\\ & f^{\mathrm{\prime }}\left(x\right)=(x-1)e^x+e^x=0\to x{e}^x=0\to x=0\end{array}$

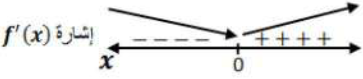
للاقتران قيمة حرجة وحيدة هي: x = 0

بما أن إشارة المشتقة الأولى تغيرت من السالب إلى الموجب عند هذه القيمة، لذا يكون للاقتران قيمة صغرى محلية هي: f (0) = -1

 

أتحقق من فهمي صفحة 106

أجد القيم القصوى المحلية (إن وجدت) للاقتران: $f\left(x\right)=\sqrt[3]{x-3}$

$\begin{array}{rl}& f\left(x\right)=\sqrt[3]{x-3}=(x-3{)}^{\frac{1}{3}}\\ & f^{\mathrm{\prime }}\left(x\right)=\frac{1}{3}(x-3{)}^{-\frac{2}{3}}=\frac{1}{3\sqrt[3]{(x-3{)}^2}}\end{array}$

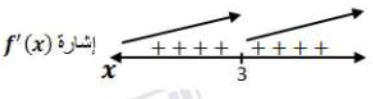
$f^{\mathrm{\prime }}\left(x\right)$  لا تساوي صفراً لأيّ عدد حقيقي x لكن $f^{\mathrm{\prime }}\left(x\right)$ غير موجودة عند x = 3 . إذن القيمة الحرجة الوحيدة هي: x = 3

الاقتران f متزايد على R ولا يوجد له قيم قصوى محلية ولا مطلقة. النقطة (3 , 0) نقطة حرجة لكنها ليست نقطة قيمة قصوى لعدم تغيّر إشارة المشتقة حولها.

---

أتحقق من فهمي صفحة 111

أجد فترات التقعّر للأعلى وللأسفل ونقاط الانعطاف (إن وجدت) لمنحنى كل اقتران ممّا يأتي:

(a) $f\left(x\right)=(x-2{)}^3(x-1)$

$\begin{array}{rl}f\left(x\right)& =(x-2{)}^3(x-1)\\ f^{\mathrm{\prime }}\left(x\right)& =(x-2{)}^3+3(x-1\left)\right(x-2{)}^2\\ f^{\prime \prime }\left(x\right)& =3(x-2{)}^2+6(x-1\left)\right(x-2)+3(x-2{)}^2\\ & =3(x-2)\left(\right(x-2)+2(x-1)+(x-2\left)\right)\\ & =3(x-2)(4x-6)=0\to x=2\text{or}x=\frac{3}{2}\end{array}$

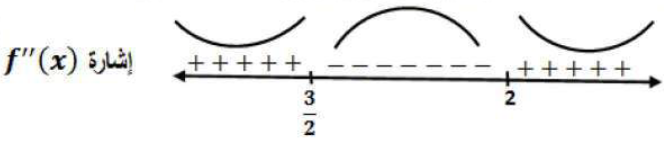
إذن منحنى f (x) مقعر للأعلى في ($-\mathrm{\infty } , \frac{3}{2}$) و ($2 , \mathrm{\infty }$)، ومقعر للأسفل في ($\frac{3}{2} , 2$) وله نقطتا انعطاف هما ($\frac{3}{2} ,-\frac{1}{16}$) و (2, 0).

 

(b) $f\left(x\right)=\frac{x}{x-1}$

$\begin{array}{rl}& f\left(x\right)=\frac{x}{x-1}\\ & f^{\mathrm{\prime }}\left(x\right)=\frac{-1}{(x-1{)}^2}\\ & f^{\prime \prime }\left(x\right)=\frac{2}{(x-1{)}^3}\end{array}$

$f^{\prime \prime }\left(x\right)$ لا تساوي صفراً لأي عدد حقيقي x ، لكن $f^{\prime \prime }\left(x\right)$ غير موجود عند x = 1

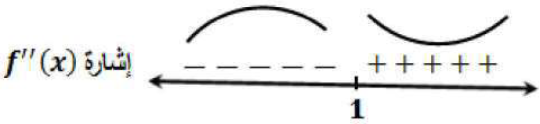
إذن منحنى f (x) مقعر للأعلى في (-∞, 1)، ومقعر للأسفل في (1, ∞) ولا توجد نقاط انعطاف مع أن المنحنى غيّر من اتجاه تقعره عند x = 1 وذلك لأنها خارج مجال f (x) .

---

اختبار المشتقة الثانية

أتحقق من فهمي صفحة 113

إذا كان  f (x) = xe^x فأستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران f .

$\begin{array}{rl}& f\left(x\right)=x{e}^x\\ & f^{\mathrm{\prime }}\left(x\right)=x{e}^x+e^x=0\to e^x(x+1)=0\to x=-1\end{array}$

القيمة الحرجة هي x = -1

$\begin{array}{rl}& f^{\prime \prime }\left(x\right)=x{e}^x+e^x+e^x=e^x(x+2)\\ & f^{\prime \prime }(-1)=e^{-1}>0\end{array}$

إذن توجد قيمة صغرى محلية للاقتران f هي f (-1) = -e^-1

---