|
أتدرب وأحل المسائل
المساحة
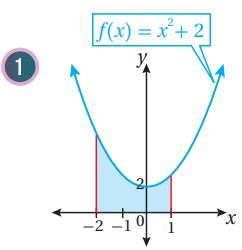
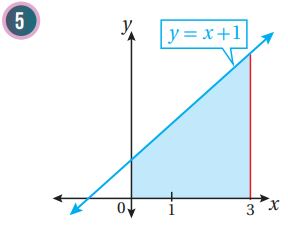
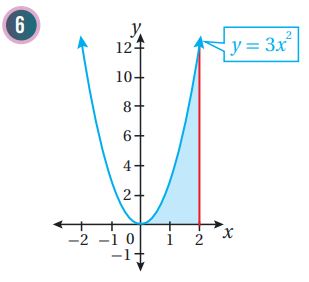
أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:
(7) أجد مساحة المنطقة المحصورة بين منحنى الاقتران:، والمحور ، والمستقيمين:
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
نحسب المميز:
بما أن المميز سالب، إذن لا يوجد حلول لهذه المعادلة، وتكون حدود التكامل هي 0 و 2 نختار عدداً ضمن الفترة [0,2]، وليكن 1 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [2,0]
إذن، المساحة هي: وحدة مربعة.
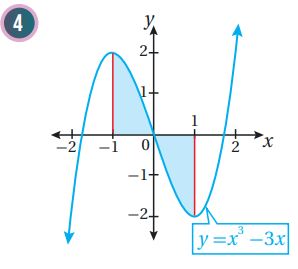
(8) جد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
هذه الإحداثيات تمثل حدود التكامل.
نختار عدداً ضمن الفترة [3,3-]، وليكن 0 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [3,3-]
إذن، المساحة هي: 36 وحدة مربعة.
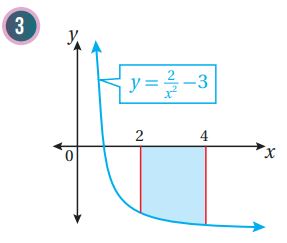
(9) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور ، والمستقيمين:
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
مميز العبارة التربيعية سالب، لذا لا أصفار لها.
نختار عدداً ضمن الفترة [1,0-]، وليكن ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض سالب، إذن منحنى الاقتران يقع تحت المحور x في الفترة [1,0-]
نختار عدداً ضمن الفترة [0,2]، وليكن 1 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [0,2]
إذن، المساحة هي: وحدة مربعة.
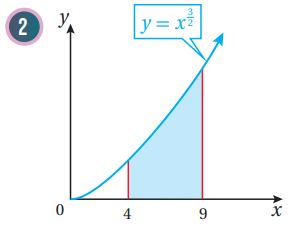
(10) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور ، والمستقيمين:
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
نحسب المميز:
بما أن المميز سالب، إذن لا يوجد حلول لهذه المعادلة، وتكون حدود التكامل هي 1 و 4 نختار عدداً ضمن الفترة [1,4]، وليكن 2 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض سالب، إذن منحنى الاقتران يقع تحت المحور x في الفترة [1,4]
إذن، المساحة هي: 27 وحدة مربعة.
(11) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور ، والمستقيمين:
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
نختار عدداً ضمن الفترة [3,5]، وليكن 4 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض موجب، إذن منحنى الاقتران يقع فوق المحور x في الفترة [3,5]
إذن، المساحة هي: 2 وحدة مربعة.
(12) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: ، والمحور
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
هذه الإحداثيات تمثل حدود التكامل.
نختار عدداً ضمن الفترة [1,4-]، وليكن 0 ونعوضه في قاعدة الاقتران:
بما أن ناتج التعويض سالب، إذن منحنى الاقتران يقع تحت المحور x في الفترة [1,4-]
إذن، المساحة هي: وحدة مربعة.
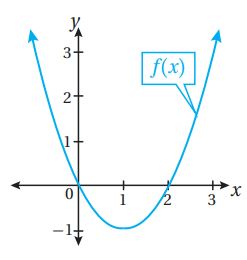
(13) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور
حسب الشكل، فإن منحنى الاقتران يقع تحت المحور x في الفترة [0,2]
إذن، المساحة هي: وحدة مربعة.
(14) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور ، والمستقيم
إذن، المساحة هي: وحدة مربعة.
(15) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور ، والمستقيم
إذن، المساحة هي: وحدة مربعة.
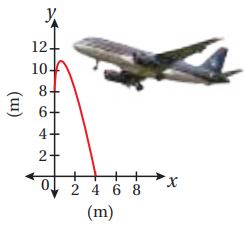
إذن، المساحة هي: وحدة مربعة.