أتدرب وأحل المسائل
التكامل بالتعويض
أجد كلاً من التكاملات الآتية:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
أجد قيمة كل من التكاملات الآتية:
(16)
(17)
(18)
(19)
(20)
(21)
أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين:
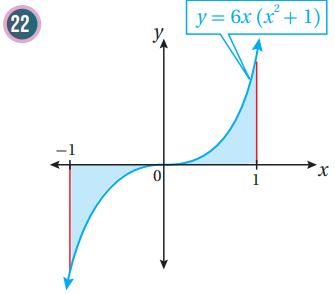
هناك طريقتان للحل: إما التكامل بالتعويض، أو تكامل كثير حدود بعد توزيع الأقواس.
طريقة التكامل بالتعويض:
ومنه مساحة المنطقة المظللة هي 9 وحدات مربعة.
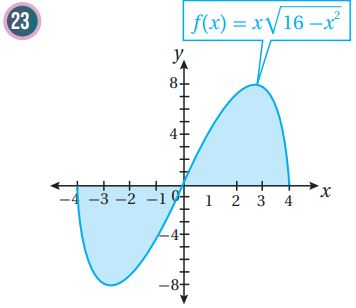
ومنه مساحة المنطقة المظللة هي وحدات مربعة.
في كل مما يأتي المشتقة الأولى للاقتران ، ونقطة يمر بها منحنى أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران :
(24)
لإيجاد ثابت التكامل، نعوض النقطة :
(25)
لإيجاد ثابت التكامل، نعوض النقطة :
(26) يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: ، حيث الزمن بالثواني، و سرعته المتجهة بالمتر لكل ثانية. إذا كان الموقع الابتدائي للجسيم ، فأجد موقع الجسيم بعد ثانية من بدء الحركة.
بما أن الموقع الابتدائي للجسيم ، إذن، :
 (27) زراعة: يمثل الاقتران سعر دونم أرض زراعية في الأغوار الأردنية (بالدينار) بعد سنة من الآن. إذا كان: هو معدل التغير في سعر دونم الأرض، فأجد ، علماً بأن سعره الآن .
(27) زراعة: يمثل الاقتران سعر دونم أرض زراعية في الأغوار الأردنية (بالدينار) بعد سنة من الآن. إذا كان: هو معدل التغير في سعر دونم الأرض، فأجد ، علماً بأن سعره الآن .
بما أن سعر دونم الأرض الآن هو 5000 دينار، إذن، ومنه:
(28) سكان: أشارت دراسة إلى أن عدد السكان في إحدى المدن يتغير سنوياً بمعدل يمكن نمذجته بالاقتران: ، حيث عدد السنوات منذ عام 2015 م، و عدد السكان بالآلاف. أجد مقدار الزيادة في عدد السكان عام 2015 م إلى عام 2025 م.
إذن يزداد عدد سكان هذه المدينة بحوالي 46 ألف شخص من 2015 م إلى 2025 م.



