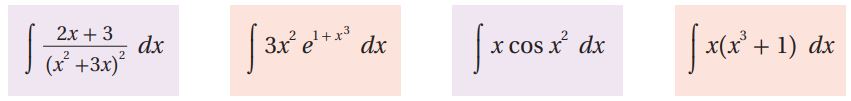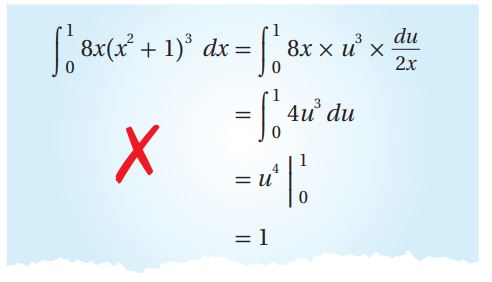مهارات التفكير العليا

مهارات التفكير العليا

التكامل بالتعويض

(29) أكتشف المختلف: التكاملات الآتية مختلف، مبرراً إجابتي؟

المختلف هو $\int x (x^{3} + 1) d x$ لأنه الوحيد الذي لا يحل بطريقة التكامل بالتعويض.

(30) أكتشف الخطأ: أوجدت سعاد ناتج التكامل: $\int_{0}^{1} 8 x {(x^{2} + 1)}^{3} d x$ ، وكان حلها على النحو الآتي:

أكتشف الخطأ للسؤال 30

أكتشف الخطأ في حل سعاد، ثم أصححه.

الخطأ الذي ارتكبته سعاد هو أنها لم تغير حدود التكامل.

$\begin{aligned} \int_{0}^{1} 8 x {(x^{2} + 1)}^{3} d x \\ u = x^{2} + 1 \Rightarrow \frac{d u}{d t} = 2 x \\ \Rightarrow d t = \frac{d u}{2 x} \\ x = 1 \Rightarrow u = 1^{2} + 1 = 2 \\ x = 0 \Rightarrow u = 0^{2} + 1 = 1 \\ \int_{0}^{1} 8 x {(x^{2} + 1)}^{3} d x = \int_{1}^{2} 8 x u^{3} \frac{d u}{2 x} \\ = \int_{1}^{2} 4 u^{3} d u \\ = {u^{4} |}_{1}^{2} \\ = (2)^{4} - (1)^{4} \\ = 15 \end{aligned}$

(31) تحد: إذ كان: $\int_{0}^{k} k x^{2} e^{x^{3}} d x = \frac{2}{3} (e^{8} - 1)$ ، فأوجد قيمة الثابت $k$ .

$\begin{aligned} \int_{0}^{k} k x^{2} e^{x^{3}} d x \\ u = x^{3} \Rightarrow \frac{d u}{d t} = 3 x^{2} \\ \Rightarrow d t = \frac{d u}{3 x^{2}} \\ x = k \Rightarrow u = k^{3} \\ x = 0 \Rightarrow u = 0^{3} = 0 \\ \int_{0}^{k} k x^{2} e^{x^{3}} d x = \int_{0}^{k^{3}} k x^{2} e^{u} \frac{d u}{3 x^{2}} \\ \int_{0}^{k} k x^{2} e^{x^{3}} d x = \frac{2}{3} (e^{8} - 1) \Rightarrow \frac{k}{3} e^{k^{3}} - \frac{k}{3} = \frac{2}{3} (e^{8} - 1) \\ = \int_{0}^{k^{3}} \frac{k}{3} e^{u} d u \\ = {\frac{k}{3} e^{u} |}_{0}^{k^{3}} - \frac{k}{3} e^{0} \\ = \frac{k}{3} e^{k^{3}} - \frac{k}{3} \end{aligned}$