أتدرب وأحل المسائل
المتجهات في الفضاء
أعيّن كلاً من النقاط الآتية في نظام الإحداثيات ثلاثي الأبعاد:
(1)
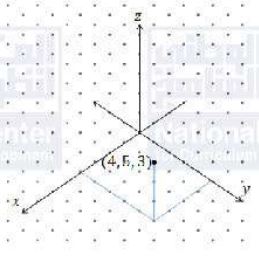
(2)
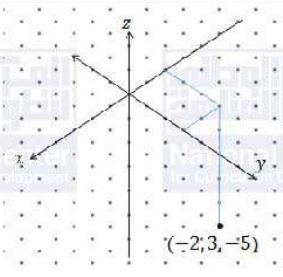
(3)
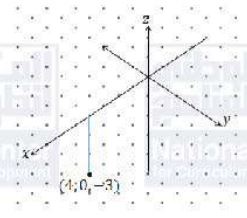
أجد الطول وإحداثيات نقطة المنتصف للقطعة المستقيمة التي أعطي طرفاها في كل مما يأتي:
(4)
(5)
(6)
(7)
أمثل كلاً من المتجهات الآتية بيانياً في الفضاء:
(8)
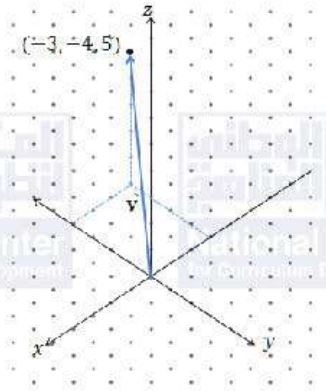
(9)
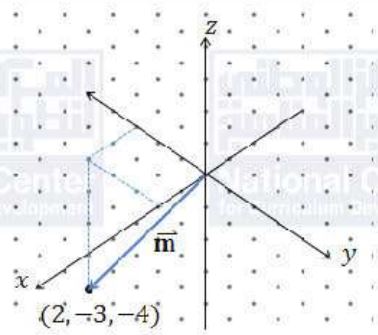
(10)
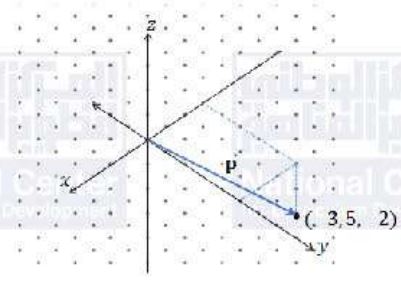
(11)
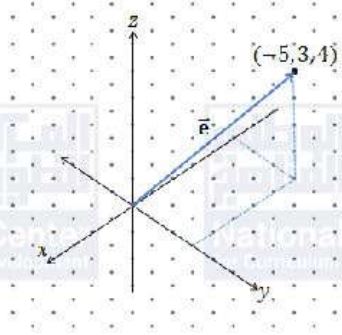
(12)
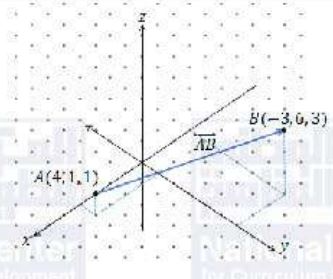
(13)
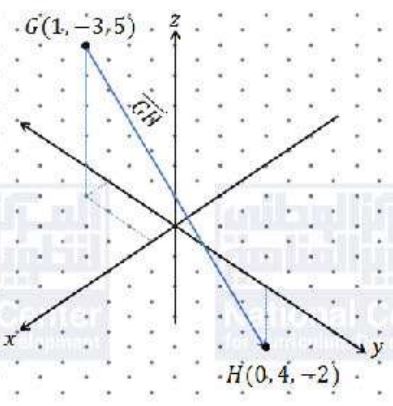
أجد الصورة الإحداثية والمقدار للمتجه الذي أعطيت نقطة بدايته ونقطة نهايته في كل مما يأتي:
(14)
(15)
(16)
(17)
(18) إذا كان OAB مثلثاً فيه: ، والنقطة C هي منتصف ، فأكتب المتجه بدلالة و.
إذا كان: ، فأجد كلاً مما يأتي:
(19)
(20)
(21)
(22)
إذا كانت: نقاطاً في الفضاء، فأجد كلاً مما يأتي:
(23) متجه موقع كل من النقاط: A وB وC.
(24) متجه الإزاحة من النقطة B إلى النقطة A.
(25) متجه الإزاحة من النقطة C إلى النقطة B.
(26) المسافة بين النقطة C والنقطة B.
أكتب كلاً من المتجهات الآنية بدلالة متجهات الوحدة الأساسية:
(27)
(28)
(29)
أجد متجه وحدة في اتجاه كل متجه مما يأتي:
(30)
وهذا هو متجه الوحدة في اتجاه
(31)
وهذا هو متجه الوحدة في اتجاه
(32)
وهذا هو متجه الوحدة في اتجاه
(33)
وهذا هو متجه الوحدة في اتجاه
(34)
وهذا هو متجه الوحدة في اتجاه
(35)
وهذا هو متجه الوحدة في اتجاه
(36) إذا كان: ، وكان: ، فأجد قيمة c.
في هذاه المعادلة يتساوى المتجهان، إذن، فإن إحداثياتهما المتناظرة متساوية:
وعند حل هذه المعادلات نجد أن لها الحل نفسه
(37) إذا كان: ، وكان: ، فأجد قيمة كل من v وw وk.
(38) إذا كان: ، فما قيمة الثابت a؟
في هذه المعادلة يتساوى المتجهان، إذن، فإن إحداثياتهما المتناظرة متساوية:
(39) إذا كان: ، وكان: ، فما قيمة u ؟
(40) إذا كان متجها الموقع للنقطة G والنقطة H هما: و، على الترتيب، فأجد قيمة c، علماً بأن: ، وأن: .
ولكن إذن،









