مهارات التفكير العليا

مهارات التفكير العليا

المتجهات في الفضاء

(39) تحد: يمر المستقيم $l_{1}$ بالنقطة Q التي متجه الموقـع لها هـو $\vec{q} = ⟨ - 6, 14, - 19 ⟩$ ، ويمر أيضا بالنقطة S التـي متجه الموقع لها هـو $\vec{s} = ⟨ - 4, 6, - 3 ⟩$ ، ويمـر المستقيم $l_{2}$ بالنقطة $T (1, 9, 9)$ ، ويوازي المستقيم: $\vec{r} = ⟨ 0, - 6, 1 ⟩ + t ⟨ 4, 7, 4 ⟩$ . إذا تقاطع المستقيم $l_{1}$ والمستقيم $l_{2}$ في النقطة U، فأثبت أن المثلث STU متطابق الضلعين.

$\vec{Q S} = ⟨ 2, - 8, 16 ⟩$

يمكن تبسيط اتجاه $\vec{Q S}$ : ${\vec{v}}_{1} = ⟨ 1, - 4, 8 ⟩$

إذن معادلة $l_{1}$ هي: $\vec{r} = ⟨ - 6, 14, - 19 ⟩ + t ⟨ 1, - 4, 8 ⟩$

معادلة $l_{2}$ هي: $\vec{r} = ⟨ 1, 9, 9 ⟩ + u ⟨ 4, 7, 4 ⟩$

لإيجاد نقطة تقاطعهما، نجد قيم u,t اللتين تجعلان $\vec{r}$ في المعادلتين متساويين:

$\begin{aligned} ⟨ - 6 + t, 14 - 4 t, - 19 + 8 t ⟩ = ⟨ 1 + 4 u, 9 + 7 u, 9 + 4 u ⟩ \\ - 6 + t = 1 + 4 u \Rightarrow t - 4 u = 7 \dots \dots \dots \dots (1) \\ 14 - 4 t = 9 + 7 u \Rightarrow 4 t + 7 u = 5 \dots \dots \dots \dots (2) \\ - 19 + 8 t = 9 + 4 u \Rightarrow 4 t - 2 u = 14 \dots \dots \dots (3) \\ (3) - (2) : 9 u = - 9 \Rightarrow u = - 1, t = 3 \end{aligned}$

وهاتان القيمتان تحققان أيضا المعادلة (1)

نجد نقطة تقاطع $l_{2}, l_{1}$ بتعويض 3=t في معادلة $l_{1}$ :

$\vec{r} = ⟨ - 6, 14, - 19 ⟩ + 3 ⟨ 1, - 4, 8 ⟩ = ⟨ - 3, 2, 5 ⟩$

إذن، نقطة تقاطع $l_{2}, l_{1}$ هي: $U (- 3, 2, 5)$

الآن لدينا أيضاً $T (1, 9, 9), S (- 4, 6, - 3)$

$\begin{aligned} T U = \sqrt{16 + 49 + 16} = 9 \\ S U = \sqrt{1 + 16 + 64} = 9 \end{aligned}$

بما أن TU=SU اذن، $△ S T U$ متطابق الضلعين.

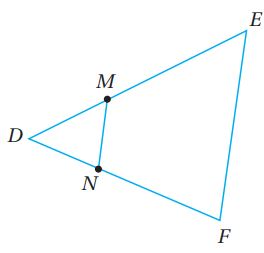تبرير: في الشكل المجاور، $D F = 8 \vec{b}, D E = 12 \vec{a}$ ، والنقطة M تقسم DE بنسبة $1 : 2$ ، والنقطة N تقسم $\bar{D F}$ بنسبة $1 : 2$

(40) أثبت أن: FEMN شبه منحرف.

$\begin{aligned} \vec{M N} = \vec{M D} + \vec{D N} = \frac{1}{3} \vec{E D} + \frac{1}{3} \vec{D F} = \frac{1}{3} (- 12 \vec{a} + 8 \vec{b}) \\ \vec{E F} = \vec{E D} + \vec{D F} = - 12 \vec{a} + 8 \vec{b} \\ \Rightarrow \vec{M N} = \frac{1}{3} \vec{E F} \end{aligned}$

وهذا يثبت أن $\vec{M N} ∥ \vec{E F}$

إذن الشكل FEMN رباعي فيه ضلعان متوازيان والضلعان الآخران غير متوازيين، فهو شبه منحرف.

(41) إذا كانت مساحة المثلث DEF تســاوي 72 وحدة مربعة، فأجد مساحة FEMN.

يمكن حل هذا السؤال بتوظيف تشابه المثلثات.

أو باستخدام مساحة المثلث بدلالة طولي ضلعين فيه وجيب الزاوية المحصورة بينهما، كالآتي:

ليكن $A_{2}$ مساحة $△ D E F$ ، $A_{1}$ مساحة $△ D M N$

$\begin{aligned} A_{2} = \frac{1}{2} (D E) (D F) \sin D \\ A_{1} = \frac{1}{2} (D M) (D N) \sin D \\ \frac{A_{2}}{A_{1}} = \frac{D N}{D F} \times \frac{D M}{D E} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9} \\ \Rightarrow \frac{A_{2}}{72} = \frac{1}{9} \Rightarrow A_{2} = 8 \end{aligned}$

مساحة شبه المنحرف FEMN تساوي: $A_{1} - A_{2} = 72 - 8 = 64$

إذن مساحة الشكل FEMN تساوي 64 وحدة مربعة.

(42) تبرير: تقع النقطة C على المستقيم الذي يحوي النقطتين: $B (22, - 22, 9), (A (13, - 10, 15)$ ، إذا كان بعد C عن B مثلي بعد C عن A، فأجد جميع إحداثيات النقطة C الممكنة، مبرراً إجابتي.

$\vec{A B} = ⟨ 9, - 12, - 6 ⟩$

يمكن تبسيط اتجاه $\vec{A B}$ : $\vec{v} = ⟨ 3, - 4, - 2 ⟩$

إذن معادلة $\vec{A B}$ هي: $\vec{r} = ⟨ 13, - 10, 15 ⟩ + t ⟨ 3, - 4, - 2 ⟩$

النقطة الواقعة على $\vec{A B}$ تكون إحداثياتها على الصورة: $C = (13 + 3 t, - 10 - 4 t, 15 - 2 t)$

$\begin{aligned} B C = 2 A C \Rightarrow (B C)^{2} = 4 (A C)^{2} \\ \Rightarrow (13 + 3 t - 22)^{2} + (- 10 - 4 t + 22)^{2} + (15 - 2 t - 9)^{2} = 4 ((3 t)^{2} + (- 4 t)^{2} + (- 2 t)^{2}) \\ \Rightarrow 87 t^{2} + 174 t - 261 = 0 \\ \Rightarrow t^{2} + 2 t - 3 = 0 \\ \Rightarrow (t + 3) (t - 1) = 0 \\ \Rightarrow t = - 3, t = 1 \\ t = - 3 \Rightarrow C (4, 2, 21) \\ t = 1 \Rightarrow C (16, - 14, 13) \end{aligned}$

(43) تحد: أجد جميع النقاط على المستقيم: $\vec{r} = ⟨ 3, - 2, - 6 ⟩ + t ⟨ 1, 2, 3 ⟩$ التي تبعد 29 وحدة عن نقطة الأصل.

النقاط الواقعة على المستقيم المعطى تكون إحداثياتها على الصورة:

$\begin{aligned} P (3 + t, - 2 + 2 t, - 6 + 3 t) \\ O P = \sqrt{(3 + t)^{2} + (- 2 + 2 t)^{2} + (- 6 + 3 t)^{2}} = 29 \end{aligned}$

نربع الطرفين ونفك الأقواس فنحصل على:

$\begin{aligned} 14 t^{2} - 38 t - 792 = 0 \\ \Rightarrow 7 t^{2} - 19 t - 396 = 0 \\ \Rightarrow (t - 9) (7 t + 44) = 0 \\ \Rightarrow t = 9, t = - \frac{44}{7} \end{aligned}$

إذن، لدينا نقطتان تحققان المطلوب هما:

$P_{1} = (12, 16, 21), P_{2} = (- \frac{23}{7}, - \frac{102}{7}, - \frac{174}{7})$

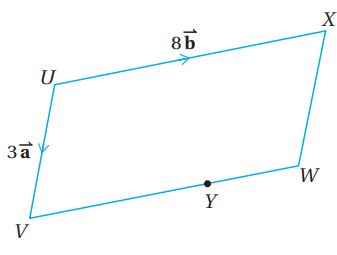(44) تحد: يمثل الشكل المجاور متوازي الأضلاع UVWX، إذا كان: $\vec{U V} = 3 \vec{a}, \vec{U X} = 8 \vec{b}$ ، وكانت النقطة لا تقع بين V و W، حيث: $V Y = 3 Y W$ ، وZ هي نقطة، حيث: $\vec{X Z} = \frac{4}{3} \vec{X W}$ ، فأثبت أن U، وY، وZ تقع على استقامة واحدة.

$\begin{aligned} \vec{X Z} = \frac{4}{3} \vec{X W} = \frac{4}{3} \vec{U V} = \frac{4}{3} (3 \vec{a}) = 4 \vec{a} \\ \Rightarrow \vec{X W} + \vec{W Z} = 4 \vec{a} \Rightarrow \vec{W Z} = 4 \vec{a} - 3 \vec{a} = \vec{a} \\ \frac{Y W}{V Y} = \frac{1}{3} \Rightarrow \frac{Y W}{V W} = \frac{1}{1 + 3} = \frac{1}{4} \Rightarrow \vec{Y W} = 2 \vec{b}, \vec{V Y} = 6 \vec{b} \\ \vec{U Y} = \vec{U V} + \vec{V Y} = 3 \vec{a} + 6 \vec{b} = 3 (\vec{a} + 2 \vec{b}) \dots \dots \dots \dots (1) \\ \vec{Y Z} = \vec{Y W} + \vec{W Z} = 2 \vec{b} + \vec{a} \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots (2) \\ \Rightarrow \vec{U Y} = 3 \vec{Y Z} \Rightarrow \vec{Y Z} ∥ \vec{U Y} \end{aligned}$

وبما أنهما ينطلقان من النقطة $Y$ إذن النقاط $U, Z, Y$ تقع على استقامة واحدة.