 |
مهارات التفكير العليا
قياس الزاوية بالراديان
تبرير: قطاع دائري طول قوسه بالسنتيمترات يساوي عددياً مساحته بالأمتار المربعة:
(35) أجد نصف قطر القطاع الدائري، مبرراً إجابتي.
نفرض طول نصف القطر بالأمتار r
(36) أجد زاوية القطاع، مبرراً إجابتي.
عدد لا نهائي من الحلول ضمن الفترة [0, 2]
(37) تبرير: أجد قياس الزاوية Ɵ في الشكل المجاور، مبرراً إجابتي.
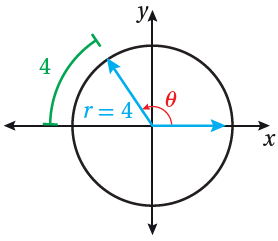
Ɵ = (π -1) rad
تحدّ: في الشكل المجاور، ACD زاوية مستقيمة، و ABE قطاع دائري مركزه B ، ونصف قطره r ، و CED قطاع دائري مركزه C ، و قائمة و :
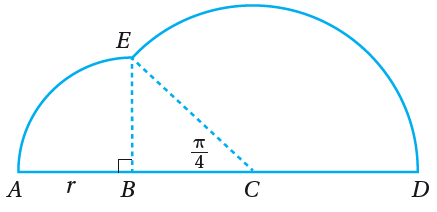
(38) أثبت أن طول هو
ABE ربع دائرة فيها AB - BE لأنهما أنصاف أقطار.
المثلث قائم الزاوية EBC فيه زاوية ، إذن فهو متطابق الضلعين، فيكون BC = r
نطبق مبرهنة فيثاغورس على المثلث قائم الزاوية EBC :
(39) أجد قياس بالراديان.
(40) أجد محيط الشكل ومساحته، علماً بأنّ r = 10 cm .
المحيط = CD + BC + AB + EA + ED
مساحة ECD + مساحة EBC + مساحة EBC = A