مهارات التفكير العليا
قاعدة السلسلة

(25) تبرير: إذا كان: ، حيث: ، وكان ، فأجد ، مبرراً إجابتي.
نجد مشتقة f ونحسب (3)
إذن:
(26) تبرير: أجد مشتقة الاقتران: y = (x2 – 4)5 عندما y = 0 ، مبرراً إجابتي؟
(27) أكتشف المختلف: أي الاقترانات الآتية مختلف، مبرراً إجابتي؟
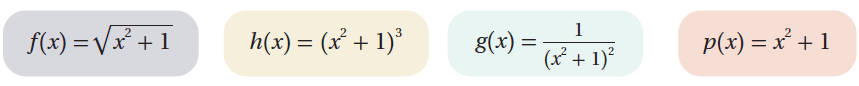
p(x) هو الاقتران الوحيد الذي يمكن اشتقاقه بدون تطبيق قاعدة السلسة.
(28) تحدّ: أجد مشتقة الاقتران: