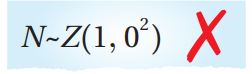|
مهارات التفكير العليا
التوزيع الطبيعي المعياري
(22) أكتشف الخطأ: عبرت روان عن المتغير العشوائي الطبيعي المعياري على النحو الآتي:
أكتشف جميع الأخطاء التي وقعت فيها روان، ثم أصححها.
(23) تحد: إذا كان ، فأثبت أن: .
تبرير: أجد قيمة التي تحقق الاحتمال المعطى في كل مما يأتي، مبرراً إجابتي:
(24)
الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية أسفل منحنى التوزيع الطبيعي.
بما أن قيمة الاحتمال أكبر من 0.5 ، فهذا يعني أن قيمة موجبة، وأنه يمكن استبدال القيمة بها.
(25)
الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية أسفل منحنى التوزيع الطبيعي.
بما أن قيمة الاحتمال أكبر من 0.5 ، فهذا يعني أن قيمة موجبة، وأنه يمكن استبدال القيمة بها.