طباعة الدرس

إجابات كتاب التمارين

التوزيع الطبيعي المعياري

أجد كلاً مما ياتي، مستعملاً جدول التوزيع الطبيعي المعياري:

$P(Z<1.42)$ (1)

$P(Z<1.42)=0.9222$

$P(Z<0.87)$ (2)

$P(Z<0.87)=0.8078$

$P(Z>1.06)$ (3)

$P(Z>1.06)=1-P(Z<1.06)=1-0.8554=0.1446$

$P(Z<-2.78)$ (4)

$P(Z<-2.78)=1-P(Z<2.78)=1-0.9973=0.0027$

$P(Z>-1.33)$ (5)

$P(Z>-1.33)=P(Z<1.33)=0.9082$

$P(1.1<Z<2.1)$ (6)

$\begin{array}{rl}P(1.1<Z<2.1)& =P(Z<2.1)-P(Z<1.1)\\ & =0.9821-0.8643=0.1178\end{array}$

$P(-2.65<Z<-1.43)$ (7)

$\begin{array}{rl}& P(-2.65<Z<-1.43)=P(Z<-1.43)-P(Z<-2.65)\\ & =1-P(Z<1.43)-(1-P(Z<2.65\left)\right)\\ & =1-0.9236-(1-0.9960)=0.0734\end{array}$

$P(0.24<Z<1.1)$ (8)

$\begin{array}{rl}P(0.24<Z<1.1)& =P(Z<1.1)-P(Z<0.24)\\ & =0.8643-0.5948=0.2695\end{array}$

$P(Z<-0.54)$ (9)

$P(Z<-0.54)=1-P(Z<0.54)=1-0.7054=0.2946$

$P(-1.8<Z<1.8)$ (10)

$\begin{array}{rl}P(-1.8<Z<1.8)=P(Z<1.8)& -P(Z<-1.8)\\ =P(Z<1.8)-(1-P(Z<1.8\left)\right)& =2P(Z<1.8)-1\\ & =2\left(0.9641\right)-1=0.9282\end{array}$

$P(Z<-1.75)$ (11)

$P(Z<-1.75)=1-P(Z<1.75)=1-0.9599=0.0401$

$P(Z>0.81)$ (12)

$P(Z>0.81)=1-P(Z<0.81)=1-0.7910=0.2080$

$P(-1<Z<-0.33)$ (13)

$\begin{array}{rl}& P(-1<Z<-0.33)=P(Z<-0.33)-P(Z<-1)\\ & =1-P(Z<0.33)-(1-P(Z<1\left)\right)\\ & =1-0.6293-(1-0.8413)=0.2120\end{array}$

$P(0.4<Z<1.7)$ (14)

$\begin{array}{rl}P(0.4<Z<1.7)& =P(Z<1.7)-P(Z<0.4)\\ & =0.9554-0.6554=0.3000\end{array}$

$P(Z>2.09)$ (15)

$P(Z>2.09)=1-P(Z<2.09)=1-0.9817=0.0183$

أجد مساحة المنطقة المظللة أسفل منحنى التوزيع الطبيعي المعياري في كل مما يأتي:

$P(0<Z<1.2)=P(Z<1.2)-P(Z<0)=0.8849-0.5=0.3849$

$\begin{array}{rl}& P(-0.5<Z<1.5)=P(Z<1.5)-P(Z<-0.5)\\ & =P(Z<1.5)-(1-P(Z<0.5\left)\right)\\ & =0.9332-(1-0.6914)=0.6246\end{array}$

$P(Z>1.6)=1-P(Z<1.6)=1-0.9452=0.0548$

$\begin{array}{rl}& P(-0.88<Z<1.65)=P(Z<1.65)-P(Z<-0.88)\\ & =P(Z<1.65)-(1-P(Z<0.88\left)\right)\\ & =0.9505-(1-0.8106)=0.7611\end{array}$

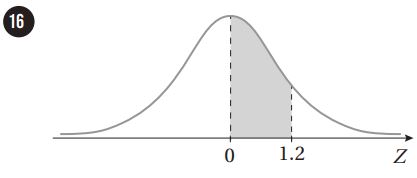
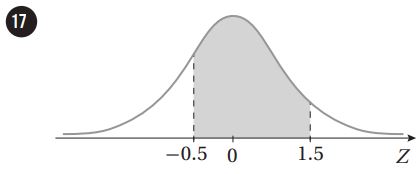
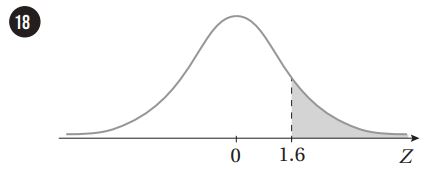
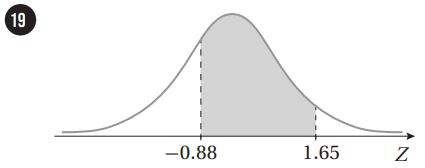
أجد قيمة $\mathit{a}$ التي تحقق الاحتمال المعطى في كل مما يأتي:

$P(Z<a)=0.9082$ (20)

الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أكبر من 0.5، فهذا يعني أن قيمة $a$ موجبة، وأنه يمكن استبدال القيمة $z$ بها.

$\begin{array}{rl}& P(Z<a)=P(Z<z)\\ & \Rightarrow 0.9082=P(Z<z)\\ & \Rightarrow z=1.33\\ & \Rightarrow a=1.33\end{array}$

$P(Z<a)=0.0314$ (21)

الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أقل من 0.5، فهذا يعني أن قيمة $a$ سالبة، وأنه يمكن استبدال القيمة $-z$ بها.

$\begin{array}{rl}& P(Z<a)=P(Z<-z)\\ & \Rightarrow 0.0314=P(Z<-z)\\ & \Rightarrow 0.0314=1-P(Z<z)\\ & P(Z<z)=1-0.0314\\ & P(Z<z)=0.9686\\ & \Rightarrow z=1.86\\ & \Rightarrow a=-1.86\end{array}$

$P(Z>a)=0.95$ (22)

الاحتمال المعطى يمثل المساحة التي تقع يمين القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أكبر من 0.5، فهذا يعني أن قيمة $a$ سالبة، وأنه يمكن استبدال القيمة $-z$ بها.

$\begin{array}{rl}& P(Z>a)=P(Z>-z)\\ & \Rightarrow 0.95=P(Z>-z)\\ & \Rightarrow 0.95=P(Z<z)\\ & \Rightarrow P(Z<z)=0.95\\ & \Rightarrow z=1.64\\ & \Rightarrow a=-1.64\end{array}$

$P(Z<a)=0.5442$ (23)

الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أكبر من 0.5، فهذا يعني أن قيمة $a$ موجبة، وأنه يمكن استبدال القيمة $z$ بها.

$\begin{array}{rl}& P(Z<a)=P(Z<z)\\ \Rightarrow & 0.5442=P(Z<z)\\ \Rightarrow & z=0.11\\ \Rightarrow & a=0.11\end{array}$

$P(Z>a)=0.2743$ (24)

الاحتمال المعطى يمثل المساحة التي تقع يمين القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أقل من 0.5، فهذا يعني أن قيمة $a$ موجبة، وأنه يمكن استبدال القيمة $z$ بها.

$\begin{array}{rl}& P(Z>a)=P(Z>z)\\ & \Rightarrow 0.2743=P(Z>z)\\ & \Rightarrow 0.2743=1-P(Z<z)\\ & \Rightarrow P(Z<z)=1-0.2743\\ & \Rightarrow P(Z<z)=0.7257\\ & \Rightarrow z=0.6\\ & \Rightarrow a=0.6\end{array}$

$P(Z>a)=0.6231$ (25)

الاحتمال المعطى يمثل المساحة التي تقع يمين القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أكبر من 0.5، فهذا يعني أن قيمة $a$ سالبة، وأنه يمكن استبدال القيمة $-z$ بها.

$\begin{array}{rl}& P(Z>a)=P(Z>-z)\\ & \Rightarrow 0.6231=P(Z>-z)\\ & \Rightarrow 0.6231=P(Z<z)\\ & \Rightarrow P(Z<z)=0.6231\\ & \Rightarrow Z=0.31\\ & \Rightarrow a=-0.31\end{array}$

(27) إذا كان $Z~N(0,1)$ وكان $P(1<Z<c)=0.1408$: فأجد قيمة الثابت $c$.

الاحتمال المعطى يمثل المساحة التي تقع يسار القيمة المعيارية $a$ أسفل منحنى التوزيع الطبيعي.

بما أن قيمة الاحتمال أكبر من 0.5، فهذا يعني أن قيمة $a$ موجبة، وأنه يمكن استبدال القيمة $z$ بها.

$\begin{array}{rl}& P(Z<c)=P(Z<z)\\ & \Rightarrow 0.9821=P(Z<z)\\ & \Rightarrow z=2.1\\ & \Rightarrow a=2.1\end{array}$