طباعة الدرس

أتحقق من فهمي

الأعداد المركبة

الوحدة التخيلية والعدد التخيلي

أتحقق من فهمي صفحة 141

أجد قيمة الجذر الرئيس في كلّ ممّا يأتي بدلالة i :

(a) $\sqrt{-75}$

$\sqrt{-75}=\sqrt{-1\times 25\times 3}=\sqrt{-1}\times \sqrt{25}\times \sqrt{3}=5i\sqrt{3}$

(b) $\sqrt{-49}$

$\sqrt{-49}=\sqrt{-1\times 49}=\sqrt{-1}\times \sqrt{49}=7i$

 

ضرب الأعداد التخيلية

أتحقق من فهمي صفحة 142

أجد ناتج كلّ ممّا يأتي في أبسط صورة مفترضاً أنّ  :

(a) $\sqrt{-27}\times \sqrt{-48}$

$\begin{array}{rl}\sqrt{-27}\times \sqrt{-48}& =\sqrt{-1\times 27}\times \sqrt{-1\times 48}\\ & =i\sqrt{9\times 3}\times i\sqrt{16\times 3}\\ & =i^2\sqrt{9\times 3\times 16\times 3}\\ & =36i^2=-36\end{array}$

(b) $\sqrt{-50}\times -4i$

$\begin{array}{rl}\sqrt{-50}\times -4i& =\sqrt{-1\times 50}\times (-4i)\\ & =5i\sqrt{2}\times (-4i)=-20\sqrt{2}{i}^2=20\sqrt{2}\end{array}$

(c) $i^{2021}$

$i^{2021}={\left(i^2\right)}^{1010}\times i=(-1{)}^{1010}\times i=i$

 

خاصية المساواة للأعداد المركبة

أتحقق من فهمي صفحة 144

أجد قيمة x ، وقيمة y الحقيقيتين اللتين تجعلان المعادلة: $x+5+(4y-9)i=12-5i$ صحيحة.

$\begin{array}{rl}x+5+(4y-9)i=12-5i& \to x+5=12 , 4y-9=-5\\ \to x=7 , y=1& \end{array}$

 

تمثيل العدد المركب ومرافقه بيانياً

أتحقق من فهمي صفحة 145

أمثّل العدد المركب ومرافقه بيانياً في المستوى المركب في كلّ ممّا يأتي:

(a) $z=2+7i$

$z=2+7i ,\overline{ z}=2-7i$

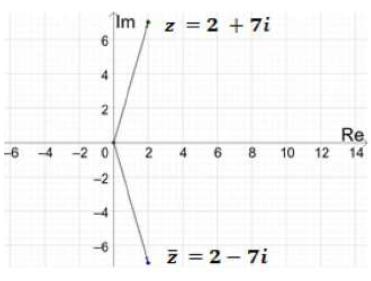
(b) $z=-3-2i$

$z=-3-2i ,\overline{ z}=-3+2i$

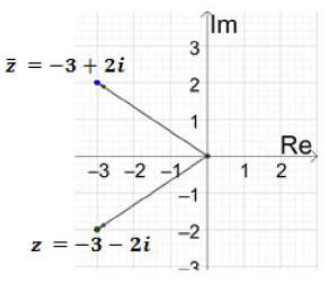
(c) $z=-3i$

$z=-3i ,\overline{ z}=3i$

 

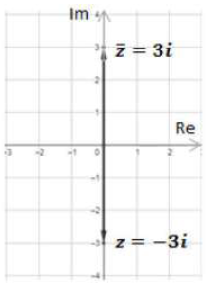
مقياس العدد المركب

أتحقق من فهمي صفحة 146

أجد مقياس كل عدد مركب ممّا يأتي:

(a) $z=-3-6i\sqrt{2}$

$z=-3-6i\sqrt{2}\to \left|z\right|=\sqrt{(-3{)}^2+(-6\sqrt{2}{)}^2}=\sqrt{81}=9$

(b) $z=-2i$

$z=-2i\to \left|z\right|=\sqrt{(0{)}^2+(-2{)}^2}=\sqrt{4}=2$

(c) $z=4+\sqrt{-20}$

$\begin{array}{rl}& z=4+\sqrt{-20}=4+\sqrt{-1}\times \sqrt{20}=4+i\sqrt{20}\\ & \to \left|z\right|=\sqrt{(4{)}^2+(\sqrt{20}{)}^2}=\sqrt{36}=6\end{array}$

 

سعة العدد المركب

أتحقق من فهمي صفحة 150

أجد سعة كل من الأعداد المركبة الآتية مقرباً إجابتي إلى أقرب منزلتين عشريتين:

(a) $z=8+2i$

$\begin{array}{rl}& z=8+2i\\ & Arg\left(z\right)=ta{n}^{-1}\left(\frac{2}{8}\right)\approx 0.24\end{array}$

(b) $z=-5+12i$

$\begin{array}{rl}& z=-5+12i\\ & Arg\left(z\right)=\pi -ta{n}^{-1}\left(\frac{12}{5}\right)\approx 1.97\end{array}$

(c) $z=-2-3i$

$\begin{array}{rl}& z=-2-3i\\ & Arg\left(z\right)=-(\pi -ta{n}^{-1}\left(\frac{3}{2}\right))\approx -2.16\end{array}$

(d) $z=8-8i\sqrt{3}$

$\begin{array}{rl}& z=8-8i\sqrt{3}\\ & Arg\left(z\right)=-ta{n}^{-1}\left(\frac{8\sqrt{3}}{8}\right)\approx -\frac{\pi }{3}\end{array}$

 

الصورة المثلثية للعدد المركب

أتحقق من فهمي صفحة 152

أكتب العدد المركب في كلّ ممّا يأتي بالصورة المثلثية:

(a) $\left|z\right|=4\sqrt{2},\mathrm{Arg}\left(z\right)=-\frac{3\pi }{4}$

$\begin{array}{rl}& \left|z\right|=4\sqrt{2},Arg\left(z\right)=-\frac{3\pi }{4}\\ & z=r(cos\theta +isin\theta )=4\sqrt{2}(cos(-\frac{3\pi }{4})+isin(-\frac{3\pi }{4}))\end{array}$

(b) $z=-4-4i$

$\begin{array}{rl}& z=-4-4i\\ & \to r=\left|z\right|=\sqrt{(-4{)}^2+(-4{)}^2}=4\sqrt{2}\\ & Arg\left(z\right)=-(\pi -ta{n}^{-1}\left(\frac{4}{4}\right))\approx -\frac{3\pi }{4}\\ & z=r(cos\theta +isin\theta )=4\sqrt{2}(cos(-\frac{3\pi }{4})+isin(-\frac{3\pi }{4}))\end{array}$

(c) $z=2i$

$\begin{array}{rl}& z=2i\\ & \to r=\left|z\right|=\sqrt{(0{)}^2+(2{)}^2}=2\\ & Arg\left(z\right)=\frac{\pi }{2}\\ & z=r(cos\theta +isin\theta )=2(cos\left(\frac{\pi }{2}\right)+isin\left(\frac{\pi }{2}\right))\end{array}$