أتدرب وأحل المسائل
التكامل بالكسور الجزئية
أجد كلاً من التكاملات الآتية:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
بجمع (1)، (2) ينتج أن: ، وبتعويض ، نجد أن
وبطرح (2) من (1) ينتج أن أي أن
بالتعويض في (3) ينتج أن:
(18)
ملاحظة: يمكن حل هذا التكامل بالتعويض
كما يمكن حله بالأجزاء حيث:
أجد قيمة كل من التكاملات الآتية:
(19)
(20)
(21)
(22)
(23)
(24)
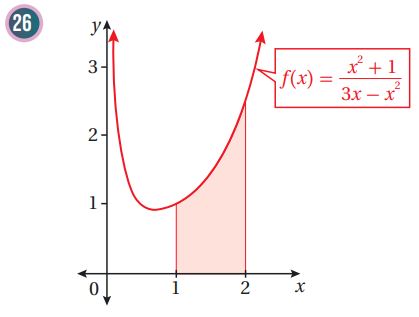
أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين:
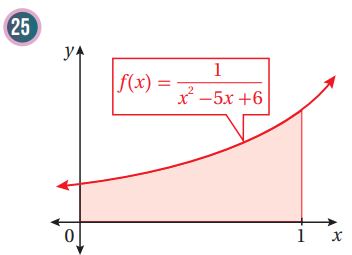
 يبين الشكل المجاور جزءاً من منحنى الاقتران: :
يبين الشكل المجاور جزءاً من منحنى الاقتران: :
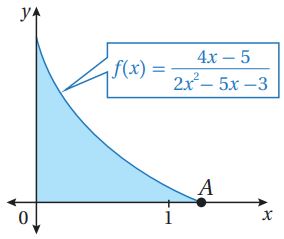
(27) أجد إحداثيي النقطة .
(28) أجد مساحة المنطقة المظللة.
ملاحظة: البسط هو مشتقة المقام، فلا داعي لتجزئة الكسر.
أجد كلاً من التكاملات الآتية:
(29)
(30)
(31)
(32)



