مسألة اليوم
المساحات والحجوم
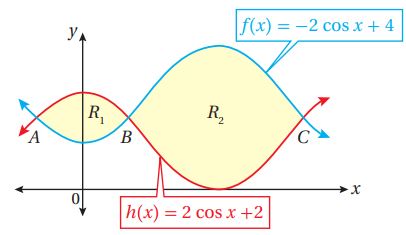 معتمداً الشكل المجاور الذي يبين منحنيي الاقترانين: ، و:
معتمداً الشكل المجاور الذي يبين منحنيي الاقترانين: ، و:
(1) أجد إحداثيي كل من النقاط: .
الإحداثي x للنقطة A هو أكبر حل سالب لهذه المعادلة وهو
إحداثيا x للنقطتين B.C هما أصغر حلين موجبين للمعادلة، وهما: و
(2) أجد مساحة كل من المنطقة ، و المنطقة .

