 |
أسئلة المحتوى وإجاباتها
القياس والأرقام المعنوية
أتحقق صفحة (20):
أحدد عناصر القياس في ما يأتي: استخدم أحمد ساعة اليد في قياس الزمن من لحظة مغادرته المنزل إلى أن وصل إلى المدرسة، فوجد أَنه (15 min).
أداة القياس: ساعة اليد.
الكمية المراد قياسها: الزمن المستغرق للوصول من البيت إلى المدرسة.
وحدة القياس: الدقيقة.
الشكل (4) صفحة (21):
حساب قراءة الميكروميتر بوحدة (mm)
أتأمل الأرقام المثبتة على الشكل، وأسجل قراءة الميكروميتر.
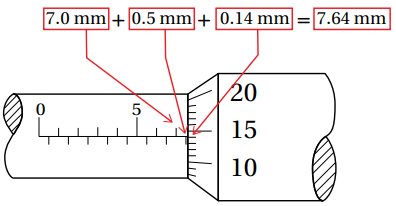
7.0 mm + 0.5 mm + 0.14 mm = 7.64 mm = 7.64 x 10-3 m
التجربة (4) صفحة (22):
أدوات القياس
التحليل والاستنتاج:
1- أتواصل مع زملائي/زميلاتي وأقارن القياسات التي حصلت عليها بالقياسات التي حصلوا عليها. هل كانت النتائج متقاربة؟
قد تختلف نتائج القياسات بمقدار بسيط من شخص إلى آخر.
2- أستنتج: لماذا قد تختلف نتيجة القياس من شخص إلى آخر؟
إجابات محتملة: نتيجة وجود أخطاء تضمنتها عملية القياس، مثل: اختلاف زاوية النظر، الاختلاف في تقدير الرقم المشكوك فيه، استخدام الأداة بطريقة غير صحيحة؛ مثلاً عدم مراعاة وضع طرف القلم عند التدريج صفر عند، استخدام المسطرة لقياس طوله.
3- أستنتج: ما أهمية اختيار الأداة المناسبة في عملية القياس؟
الحصول على نتيجة قياس دقيقة.
أتحقق صفحة (22):
أذكر أمرين يجب أخذهما في الحسبان عند اختيار أداة القياس.
اختيار الأداة المناسبة للكمية المراد قياسها، ومعرفة أصغر تدريج يقرؤه الجهاز أو الأداة.
أفكر صفحة (22):
باستخدام الأدوات الآتية: ورقة بيضاء، قلم، خيط صوف، مسطرة، مقص. أصمم تجربةً، لقياس محيط قرص دائري، وأوضح الأمور التي سأعمل بمقتضاها لزيادة دقة القياس ما أمكن.
أضع القرص على سطح الطاولة (على الورقة)، وألف الخيط حول محيطه، وأقص طرفه. ثم أقيس طول قطعة الخيط بالمسطرة. ولزيادة دقة القياس؛ أكرر التجربة ثلاث مرات وأحسب الوسط الحسابي للقياسات حصلت عليها. وأراعي عند استخدام المسطرة شد الخيط وتثبيت أحد طرفيه عند تدريج الصفر تماماً، وقراءة التدريج المقابل للطرف الثاني للخيط والذي يمثل محيط القرص.
أفكر صفحة (24):
أفكر استخدمت نور مسطرة لقياس طول جسم، وعبرت عن القياس بالمقدار (12.350 cm). فإذا كان أكبر تدريج يظهر على المسطرة (30 cm) وأصغر تدريج (1 mm)، فهل النتيجة مقبولة علمياً؟ أفسر إجابتي.
المسطرة مدرجة بوحدة السنتيمتر وأكبر تدريج يظهر عليها (30 cm) واستخدمت لقياس جسم طوله (12 cm) تقريباً فهي أداة مناسبة لقياس طول الجسم. لكن القياس الذي سجلته الطالبة (12.350) غير مقبول؛ فأصغر تدريج يظهر على المسطرة (1 mm)، لذا فالمسطرة لا تقيس أجزاء المليمتر؛ بل تسمح بتقديرها. لذا فإن الرقم الذي يقع في منزلة أجزاء المليمتر (0.05) رقم مشكوك فيه ولا يمكن تأكيده بإضافة صفر في المنزلة التي تليه.
تمرين صفحة (26):
أحدد عدد الأرقام المعنوية في كل من القياسات الآتية:
أ- 202 mm
3 أرقام معنوية.
ب- 1.25 cm
4 أرقام معنوية.
ج- 0.050 mm
رقمان معنويان.
د- 6.01 x 10-3 m
3 أرقام معنوية.
أتحقق صفحة (27):
أحسب الناتج وأعبر عنه بعددٍ مناسب من الأرقام المعنوية:
34.8 cm – 5.9 cm
العشرية في كلا الرقمين؛ منزلة واحدة. وبإيجاد ناتج الطرح نجد أن:
34.8 – 5.9 = 28.9
أتحقق صفحة (28):
ما عدد الأرقام المعنويّة التي يجب أن تحتويها الإجابة عند ضرب القياسين )(8.8cm ، )23.6cm.(
رقمان معنويان.
أفكر صفحة (28):
يبين الشكل عملية حسابية أجريت باستخدام آلة حاسبة.

أتبع قواعد التعامل مع الأرقام المعنوية لأعبر عن الإجابة بالعدد المناسب من الأرقام المعنوية.
في عملية الطرح يجب أن يكون عدد المنازل العشرية مساوياً لعدد المنازل العشرية الأقل في الكميات المعطاة؛ وهو في هذه الحالة منزلة عشرية واحدة وبتدوير الإجابة يكون الناتج (89.3 cm).