أسئلة المحتوى وإجاباتها

الحركة في بعد واحد

تجربة استهلالية صفحة (41):

وصف الحركة باستخدام المدرج الهوائي

التحليل والاستنتاج:

1- أحد الزمن الكلي لحركة العربة في حال استخدام كل كتلة.

قراءة زمن الحركة الكلي من العداد الرقمي، ومراعاة أن تكون دقة القياس (0.1 s).

2- أجد ناتج قسمة إزاحة العربة على زمن الحركة في كل من الحالتين (الناتج هو السرعة المتوسطة).

العلاقة الرياضية اللازمة لحساب السرعة المتوسطة، وهي ناتج قسمة الإزاحة الكلية للعربة على الزمن الكلي.

3- أقارن النتائج عند اختلاف الكتلة المعلقة.

سيؤدي تغيير الكتلة المعلقة بأخرى أكبر منها إلى زيادة القوة المؤثرة في العربة، وزيادة تسارعها، وزيادة مقدار السرعة المتوسطة.

4- التفكير الناقد: إذا كانت سرعة العربة الابتدائية صفراً، فهل يمكن معرفة سرعتها النهائية بناءً على سرعتها المتوسطة؟

تفكير ناقد تُحسب السرعة النهائية بمعرفة كل من السرعة المتوسطة والسرعة الابتدائية، يفترض في هذه التجربة أن تكون السرعة الابتدائية مساوية للصفر)، وذلك باستخدام العلاقة الآتية: السرعة المتوسطة = صفراً + السرعة النهائية) ÷ 2

أفكر صفحة (43):

هل يستطيع جسمٌ متحركٌ أن يغير موقعه أكثر من مرّة بحيث تكون إزاحته صفراً؟ أوضّح إجابتي.

نعم، ذلك ممكن؛ فعندما يتحرك الجسم من موقع ابتدائي إلى موقع آخر، ثم يتحرك مرّة أخرى إلى موقعه الابتدائي، فإن إزاحته تساوي صفراً، وكذلك يساوي متجه التغير في الموقع صفراً. (لاحظ هنا أنّ المسافة لا تساوي صفراً).

أتحقق صفحة (43):

فيمَ تختلف المسافة التي قطعتها الكرة عن الإزاحة التي أحدثتها في هذه الحركة؟ أيّهما أكبر: المسافة أم مقدار الإزاحة؟

تتضمن إجابة السؤال الصحيحة وجود اختلافين؛ أولهما أنّ الإزاحة كمية متجهة والمسافة كميّة قياسية، وثانيهما أنّ مقدار الإزاحة ليس بالضرورة أن يتساوى مع المسافة. وفي هذه الحالة كان مقدار الإزاحة (6 m)، والمسافة (12 m)؛ أيّ أنّ المسافة التي قطعتها الكرة كانت أكبر من مقدار الإزاحة الناتجة من تغير موقع الكرة، ودائماً تكون المسافة أكبر من مقدار الإزاحة، أو تساويه.

 أتحقق صفحة (44):

أقارن بين السرعة القياسية المتوسطة والسرعة المتجهة المتوسطة من حيث: وحدة القياس، الاتجاه، رمز كل منهما.

تُقاس إلى السرعة القياسية المتوسطة بوحدة (m/s) وليس لها اتجاه، ويرمز لها بالرمز ($\overline{v}$_s)، حيث يشير حرف (s) إلى كلمة (speed)؛ لتمييزها من السرعة المتجهة، والسرعة المتجهة المتوسطة تُقاس بالوحدة نفسها (m/s)، ولها اتجاه، ويُرمز لها بالرمز ($\overline{v}$).

أتحقق صفحة (45):

ما الشرط الواجب توافره في الحركة في بعدٍ واحدٍ لكي تتساوى السرعة المتجهة المتوسطة مع السرعة اللحظية؟

عندما تكون الحركة في بعدٍ واحدٍ فإنّ المسافة تساوي مقدار الإزاحة، ويشترط لذلك أن تكون الحركة محددة في اتجاهٍ واحدٍ.

أفكر صفحة (47):

عندما تزداد سرعة السيارة بمقدار (2 m/s) في كل ثانية يكون التسارع ثابتًا. كيف يكون تسارع السيارة غير ثابت؟

عندما تزداد سرعة السيارة بمقادير مختلفة في مدد زمنية متساوية يكون تسارعها غير ثابت، ويحدث ذلك على سبيل المثال؛ بأن تزداد السرعة خلال الثانية الأولى بمقدار (3 m/s) ثم تزداد خلال الثانية الثانية بمقدار (5 m/s) وقد تقل خلال الثانية الثالثة بمقدار (1.5 m/s).

أتحقق صفحة (48):

أجد التسارع المتوسط لكل من السيارتين في أثناء مُدد زمنية أخرى؛ من: (t₁ = 0 s) إلى (t₄ = 3 s) مثلاً.

الإجابة لن تختلف عن الإجابة في المثال (3)؛ لأن السيارة الأولى تتحرك بسرعة ثابتة (تسارع ثابت يساوي صفراً)، والسيارة الثانية تسارعها ثابت؛ لأن سرعتها تزداد بصورة منتظمة (بمقدار: 2 m/s في كل ثانية). وعندما يكون التسارع ثابتاً فإنّ التسارع المتوسط يكون ثابتاً أيضاً، ويساوي التسارع اللحظي.

أتحقق صفحة (50):

بدأت طائرة السير على مدرج المطار من وضع السكون، بحركة أفقية في خطٍ مستقيم، فأصبحت سرعتها (80 m/s) بعد مرور مدّة زمنية مقدارها ( = 32 st). أجد مقدار التسارع المتوسط للطائرة في أثناء تلك المدّة، ثم أحدد اتجاهه.

في هذا المثال تكون السرعة الابتدائية والسرعة النهائية في الاتجاه نفسه، فيكون التغير في السرعة والتسارع في اتجاه السرعة.

أتحقق صفحة (52):

أصف شكل منحنى الموقع-الزمن لجسمٍ يتحرك بسرعة ثابتة؛ مقداراً، واتجاهاً.

تكون العلاقة على شكل خط مستقيم، ميله ثابت، لا يساوي صفراً.

الشكل (6) صفحة (53):

منحنى السرعة - الزمن.

ما مقدار سرعة الجسم عند الثانية (5 s)؟

عند اللحظة الزمنية (5 s) ، أقيم عمودًا على محور الزمن، حتى يتقاطع مع منحنى العلاقة. ثم أرسم خطا أفقياً باتجاه محور السرعة، فيتقاطع معه عند التدريج (3 m/s) وهذا هو مقدار السرعة عند تلك اللحظة.

 أتحقق صفحة (53):

كيف أحدد ما إذا كان الجسم يتسارع أم يتباطأ من منحنى (السرعة - الزمن)؟

عندما يكون ميل المنحنى موجبًا؛ فهذا يعني أن السرعة تزداد مع الزمن، ويكون الجسم متسارعًا، وعندما يكون الميل سالبًا؛ فهذا يعني أن السرعة تقل مع الزمن؛ ويكون الجسم متباطئًا.

أفكر صفحة (56):

في الحركة بتسارع ثابت، حيث يكون التغير في السرعة منتظماً، تتساوى السرعة المتوسطة مع المتوسط الحسابي للسرعتين الابتدائية والنهائية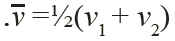

لماذا لا يكون ذلك صحيحاً عندما تتغير السرعة على نحوٍ غير منتظم؟

عندما تتغير سرعة الجسم بشكل منتظم (يكون التسارع متغيراً) فإن المتوسط الحسابي للسرعتين الابتدائية والنهائية لا يمثل السرعة المتوسطة؛ لأن اعتماد السرعة على الزمن ليس خطياً، ما يتطلب أخذ مزيد من قيم السرعة في أوقات زمنية متماثلة؛ كأنْ تكون عشر قيم، ثم تجمع، ويقسم المجموع على عددها، فينتج المتوسط الحسابي لها جميعاً، الذي يمثل السرعة المتوسطة.

أتحقق صفحة (58):

متى يمكنني استخدام معادلات الحركة الثلاث السابقة؟

عند حركة الجسم بتسارع ثابت.

تمرين صفحة (58):

في المثال السابق، أجد المدة الزمنية التي قطع فيها القطار الإزاحة المذكورة.

المعطيات:

السرعة الابتدائية: (20 m/s = v₁).

السرعة النهائية: (4 m/s = v₂).

التسارع: )1.5 m/s²- = a).

المطلوب: )t = ??(

الحل:

v₂ = v₁ + at

4 = 20 + (-1.5) x t

t = $\frac{-16}{-1.5}$ = 10.67 s

تجربة (1) صفحة (60):

قياس تسارع السقوط الحر عمليًّا

التحليل والاستنتاج:

1- أقارن: بالتعاون مع أفراد مجموعتي، أقارن النتيجة التي توصلنا إليها عمليًّا بالقيمة المقبولة المتفق عليها (9.8 m/s²).

مقارنة النتيجة بالقيمة المعتمدة، وملاحظة الاختلاف في النتائج. هل جميع نتائج المجموعات أكبر من (9.8 m/s)، أم أقل منه، أم أن بعضها أكبر من ذلك، وبعضها الآخر أقل منه؟

2- أستنتج: ما سبب اختلاف النتيجة بين مجموعةٍ وأخرى؟ ما سبب اختلاف النتيجة عن القيمة المقبولة؟

البحث في معرفة مصادر الخطأ، التي قد تنجم عن إسقاط الكرة من مكان أعلى من البوابة الضوئية العليا، أو استخدام كرة خفيفة الوزن تتأثر بمقاومة الهواء لحركتها، أو وجود خطأ في توصيل البوابتين بالعداد.

3- أفسر: ما سبب اختيار كرةٍ مطاطية صغيرة الحجم؟ إذا استخدمت كرة كبيرة الحجم وخفيفة، فما الذي سيتغير.

حتى تكون مساحة مقطعها صغيرة، ويمكننا إهمال مقاومة الهواء؛ حيث إن الكرة الكبيرة يظهر تأثير مقاومة الهواء لها.

أتحقق صفحة (61):

ما القوة المؤثرة في جسم يسقط سقوطاً حراً؟

الوزن هو القوة الوحيدة المؤثرة في الجسم في حالة السقوط الحرّ؛ وذلك بإهمال تأثير مقاومة الهواء لحركة الجسم.