مهارات التفكير العليا
مهارات التفكير العليا
المساحة
أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:
حسب الشكل، فإن منحنى الاقتران يقع فوق المحور x في الفترة [0,4]
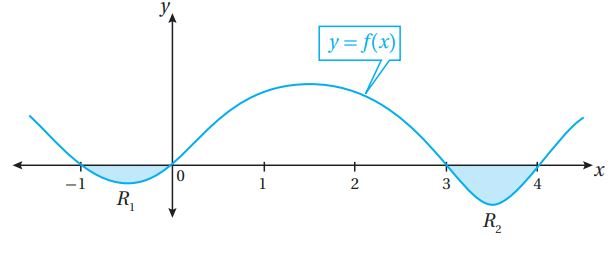
(18) تبرير: يبين الشكل التالي منحنى الاقتران . إذا كانت مساحة المنطقة هي وحدتين مربعتين، ومساحة لمنطقة هي 3 وحدات مربعة ، وكان : ، فأجد ، مبرراً إجابتي.
إعداد : شبكة منهاجي التعليمية
10 / 02 / 2023
النقاشات