أتدرب وأحل المسائل
الاقترانات المتشعبة
إذا كان: ، وكان:
فأجيب عن الأسئلة الآتية:
(1) أحدد مجال كل من: f(x) ، و g(x)
مجال الاقتران f هو جميع قيم x الحقيقية.
مجال الاقتران g هو جميع قيم x الحقيقية التي تنتمي للفترة (∞-3, ) ما عدا العدد 0.
(2) أجد قيمة كل من: f(-1) ، و f(2) ، و g(0) ، و g(-2)
g(0) , f(2) = 2 , f(-1) = 2 غير معرّف، g(-2) = -3
(3) أمثل الاقتران: f(x) بيانياً، ثم أحدد مداه.
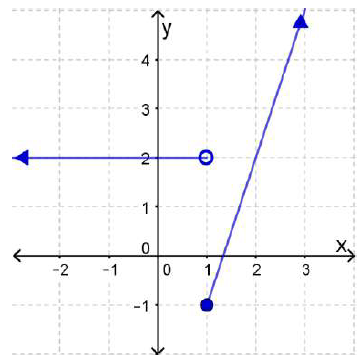
المدى هو جميع قيم y التي تنتمي للفترة (-1, ).
(4) أمثل الاقتران: g(x) بيانياً، ثم أحدد مداه.
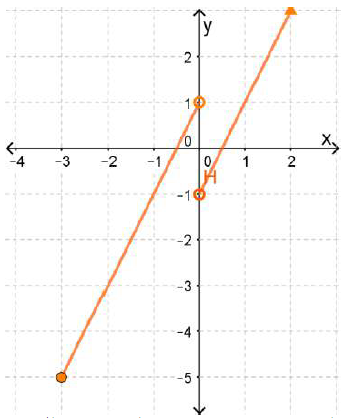
المدى هو جميع قيم y التي تنتمي للفترة (-5, ) ما عدا -1 , 1
أكتب قاعدة الاقتران المتشعب الممثل بيانياً في كل مما يأتي:
(5)
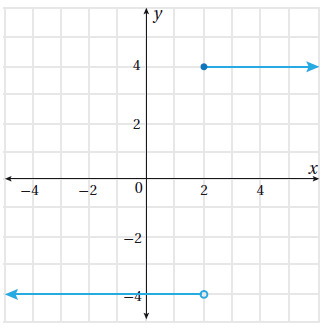
(6)
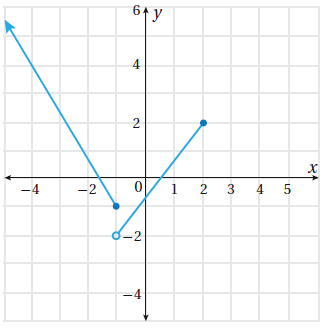
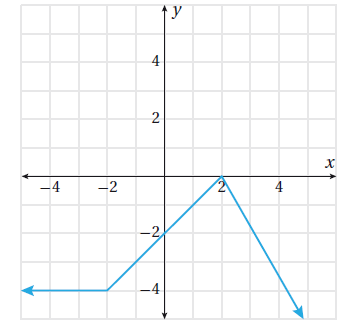 معتمداً الشكل المجاور الذي يمثل منحنى الاقتران المتشعب h(x) ، أجيب عن السؤالين الآتيين:
معتمداً الشكل المجاور الذي يمثل منحنى الاقتران المتشعب h(x) ، أجيب عن السؤالين الآتيين:
(7) أحدد مجال الاقتران h(x) ، ومداه.
(8) أجد قيمة كل من: h(-3) ، و h(0) ، و h(3) ، و h(6)
 (9) توفير: أراد الوالدُ أن يُحفّز ابنته على توفير جزء من مصروفها اليومي فقرر منحها مبلغاً يساوي ما ستوفره نهاية كل شهر في حال لم يتجاوز مبلغ التوفير JD 5 . أمّا إذا زاد على ذلك فإنه سيمنحها JD 10 . أكتب اقتراناً متشعباً يمكن استعماله لتمثيل هذا الموقف.
(9) توفير: أراد الوالدُ أن يُحفّز ابنته على توفير جزء من مصروفها اليومي فقرر منحها مبلغاً يساوي ما ستوفره نهاية كل شهر في حال لم يتجاوز مبلغ التوفير JD 5 . أمّا إذا زاد على ذلك فإنه سيمنحها JD 10 . أكتب اقتراناً متشعباً يمكن استعماله لتمثيل هذا الموقف.
 (10) أعمال: يعمل مندوب مبيعات لدى شركة لقاء راتب شهري مقداره JD 500 ، وعمولة شهرية نسبتها 1% عن أول JD 2000 لثمن مبيعاته. وفي حال زادت المبيعات الشهرية على JD 2000 ، فإنه يستحق عمولة نسبتها 1.5% عن المبلغ الذي يزيد على JD 2000 . أكتب اقتراناً متشعباً يمكن استعمال لحساب الدخل الشهري لمندوب المبيعات.
(10) أعمال: يعمل مندوب مبيعات لدى شركة لقاء راتب شهري مقداره JD 500 ، وعمولة شهرية نسبتها 1% عن أول JD 2000 لثمن مبيعاته. وفي حال زادت المبيعات الشهرية على JD 2000 ، فإنه يستحق عمولة نسبتها 1.5% عن المبلغ الذي يزيد على JD 2000 . أكتب اقتراناً متشعباً يمكن استعمال لحساب الدخل الشهري لمندوب المبيعات.
(11) أحل المسألة الواردة في بند (مسألة اليوم).
7300 ديناراً.
إعداد : شبكة منهاجي التعليمية
18 / 02 / 2023
النقاشات