أتدرب وأحل المسائل
مساحة الدائرة
أَجد مساحة كل دائرة ممّا يأتي، وأستعمل الآلة الحاسبة لأتحقق من صحة إجابتي:
(1)
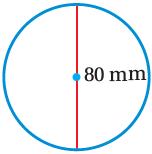
A = πr2
A = 3.14 x (40)2
A = 5024 mm2
(2)
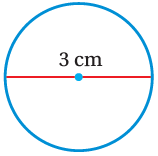
A = πr2
A = 3.14 x (1.5)2
A = 7.065 cm2
(3)
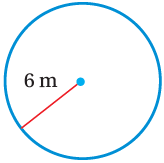
A = πr2
A = 3.14 x (6)2
A = 113.04 m2
(4) أَجِدُ طول نصفِ قُطْرِ دائرة مساحتها 314 cm2، أستعمل π ≈ 3.14
A = πr2
314 = 3.14 x r2
أقسم الطرفين على 3.14 :
100 = r2
r = 10 cm
(5) أَجِدُ مساحة نصف الدائرة الظاهر في الشكل المجاور.
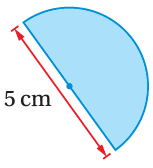
A = πr2
A = 3.14 x (2.5)2
A = 19.625 cm2
أقسم المساحة المحسوبة على (2) لإيجاد مساحة نصف الدائرة:
A = 9.8125 cm2
(6) صحة: إذا كان طول قطر الزجاجة الدائرية في جهاز قياس ضغط الدم 18 cm، أجد مساحتها.

A = πr2
A = 3.14 x (9)2
A = 254.34 cm2
(7) مراوح: تتكون المروحة المجاورة من 4 أجزاء متطابقة كل جزء منهـا عـلـى شـكـل ربـع دائرة، ودائرة داخلية، أجد مساحة سطح المروحة الخارجي.
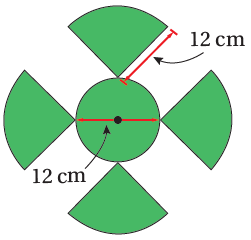
أجد مساحة القطع الـ (4) المتطابقة والتي تشكل معاً دائرة نصف الدائرة 12 cm :
A = πr2
A = 3.14 x (12)2
A = 452.16 cm2
أجد مساحة الدائرة الداخلية والتي نصف قطرها 6 cm :
A = πr2
A = 3.14 x (6)2
A = 113.04 cm2
أجمع مساحة القطع الـ (4) المتطابقة مع مساحة الدائرة الداخلية:
A = 452.16 cm2 + 113.04 cm2 = 565.2 cm2
(8) دراجة: تقطعُ عَجلة درّاجة مسافة 197 cm في كل دورة كاملة لها، أَجِدُ مساحة الدائرة التي لها قطرُ العجلة نفسه. أقرب إجابتي لأقرب عددٍ صحيح.
تمثل المسافة 197 cm محيط الدائرة:
C = πd
197 = 3.14 x d
d ≈ 62.74 cm
إذن: قطر الدائرة 62.74 cm :
أحسب مساحة الدائرة التي نصف قطرها 31.37 cm :
A = πr2
A = 3.14 x (31.37)2
A = 3090 cm2
(9) عقد: صنعت ريماسُ عِقدًا باستعمال دائرتين. لوّنَتْ جزءًا مِنَ العِقد باللون الأصفر مثلما يظهر في الشكل المجاور، أحسب مساحة الجزء الذي لونته ريماس مقرباً إجابتي لأقرب جزء من عشرة.
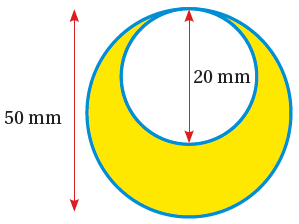
أحسب مساحة الدائرة الصغرى التي نصف قطرها 10 mm :
A = πr2
A = 3.14 x (10)2
A = 314 mm2
أحسب مساحة الدائرة الكبرى (الصفراء) التي نصف قطرها 25 mm :
A = πr2
A = 3.14 x (25)2
A = 1962.5 mm2
أطرح مساحة الدائرة الصغرى من مساحة الدائرة الكبرى:
1962.5 – 314 = 1648.5 mm2
وتمثل المساحة المحسوبة مساحة الجزء الذي لونته ريماس.
(10) أجد مساحة المنطقة المظللة في الشكل الآتي. أقرب إجابتي لأقرب جزء من عشرة.
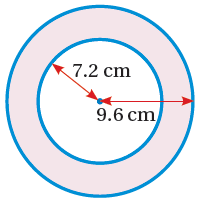
أحسب مساحة الدائرة الصغرى التي نصف قطرها 7.2 cm :
A = πr2
A = 3.14 x (7.2)2
A ≈ 162.78 cm2
أحسب مساحة الدائرة الكبرى التي نصف قطرها 9.6 cm :
A = πr2
A = 3.14 x (9.6)2
A ≈ 289.38 cm2
أطرح مساحة الدائرة الصغرى من مساحة الدائرة الكبرى:
289.38 – 162.78 = 126.6 cm2
وتمثل المساحة المحسوبة مساحة المنطقة المظللة.
(11) فطائر: أعود إلى فقرة (أستكشف) بداية الدرس وأحل المسألة.
أعلن محل بيع فطائر عَنْ عرضِ لِبيعِ فَطيرة بيتزا كبيرة طول قطرها 30 cm بسعر JD 7.99، وفطيرَتَيْ بيتزا متوسطتين طول قطر كل واحدةٍ 20 cm بسعر JD 7.99، أيُّ العرضين أفضل؟

أحسب مساحة فطيرة البيتزا الكبيرة:
A = πr2
A = 3.14 x (15)2
A = 706.5 cm2
أحسب مساحة فطيرة البيتزا المتوسطة:
A = πr2
A = 3.14 x (10)2
A = 314 cm2
أحسب مساحة فطيرتي البيتزا:
A = 2 x 314 = 628 cm2
إذن: عرض فطيرة البيتزا الكبيرة أفضل.
إعداد : شبكة منهاجي التعليمية
31 / 03 / 2023
النقاشات
شروق عبدالقادر
شكرا على كل حال وفي كل مكان في العالم
إضافة رد
0 ردود