أتحقق من فهمي
المساحات والحجوم
مساحة المنطقة المحصورة بين منحنيي اقترانين
أتحقق من فهمي صفحة (77):
(a) أجد مساحة المنطقة المحصورة بين منحنيي اقترانين: ، والمستقيمين .
هذه المعادلة ليس لها حلول إذ أن المنحنيين لا يتقاطعان كما في الشكل أدناه.
(b) أجد مساحة المنطقة المحصورة بين منحنيي اقترانين: ، والمستقيمين .
نجد أن لكل قيم x، إذن:
أتحقق من فهمي صفحة (79):
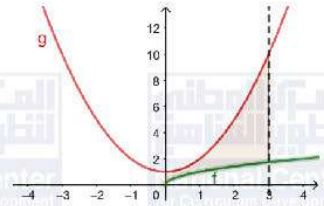
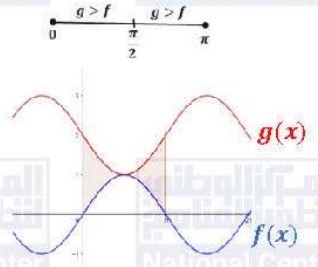
أجد مساحة المنطقة المحصورة بين منحنيي اقترانين: .
نلاحظ أن في الفترة إذن:
التكامل، ومنحنى السرعة المتجهة - الزمن
أتحقق من فهمي صفحة (81):
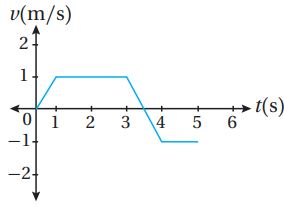
(a) إزاحة الجسيم في الفترة الزمنية المعطاة.
لتكن الإزاحة D
(b) المسافة التي قطعها الجسيم في الفترة الزمنية المعطاة.
المساحة التي قطعها الجسيم هي:
(c) الموقع النهائي للجسيم.
في الفرع a وجدنا أن:
وبتعويض نجد أن:
الحجوم الدورانية
أتحقق من فهمي صفحة (82):
أجد حجم المجسم الناتج من دوران المنطقة المحصورة بين منحنى الاقتران: ، والمحور ، والمستقيمين ، حول المحور .
حجم المجسم الدوراني الناتج من دوران منحنيي اقترانين
أتحقق من فهمي صفحة (85):
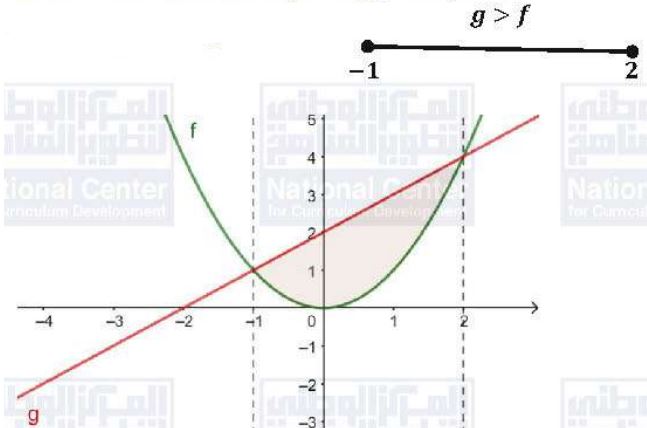
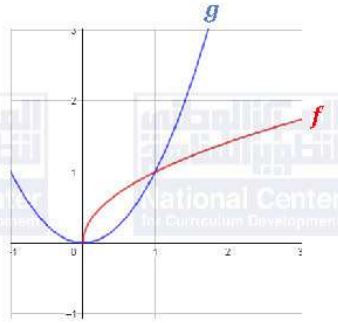
أجد حجم المجسم الناتج من دوران المنطقة المحصورة بين منحنيي الاقترانين: ، و ، حول المحور .
انلاحظ أن منحنى f يقع فوق منحنى g في الفترة [0,1]
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات