إجابات أسئلة مراجعة الوحدة
الشغل والطاقة
أينما يلزم يكون تسارع السقوط الحر (g = 10 m/s2)، ما لم يُذكر غير ذلك.
السؤال الأول:
أضع دائرة حول رمز الإجابة الصحيحة لكل جملة ممّا يأتي:
1- الشغل الذي تبذله قوة مقدارها (1 N) عندما تؤثر في جسم وتحركه إزاحة مقدارها (1 M) في اتجاهها، يُسمى:
أ- النيوتن (N).
ب- الجول (J).
ج- الواط (W).
د- الحصان (hp).
2- مقدرة الجسم على بذل شغل، تُسمى:
أ- الطاقة.
ب- الشغل.
ج- القدرة.
د- القوة المحصلة.
3- الطاقة المختزنة في جسم نتيجة موقعه بالنسبة إلى مستوى إسناد، تُسمى:
أ- الشغل.
ب- الطاقة الحركية.
ج- القدرة.
د- طاقة الوضع الناشئة عن الجاذبية.
توضح الأشكال الثلاثة الآتية، انزلاق 3 صناديق مختلفة الكتل من السكون، من الارتفاع نفسه على مستويات مائلة ملساء لها الميل نفسه. أستعين بهذه الأشكال للإجابة عن الأسئلة (7-4):
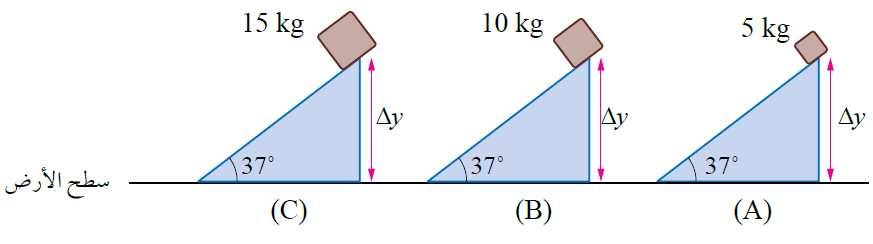
4- الصندوق الذي له أكبر طاقة وضع ناشئة عن الجاذبية، هو:
أ- A.
ب- B.
ج- C.
د- طاقات وضعها جميعها متساوية.
5- الترتيب الصحيح للطاقة الحركية للصناديق الثلاثة لحظة وصولها إلى سطح الأرض، هو:
أ- KEA > KEB > KEC
ب- KEC > KEB > KEA
ج- KEB > KEA > KEC
د- طاقات وضعها جميعها متساوية.
6- الصندوق الذي له أكبر سرعة لحظة وصوله إلى سطح الأرض، هو:
أ- A.
ب- B.
ج- C.
د- سرعتها جميعها متساوية.
7- الصندوق الذي يصل إلى سطح الأرض أولاً، هو:
أ- A.
ب- B.
ج- C.
د- تصل جميعها إلى سطح الأرض في اللحظة نفسها.
8- تكون الطاقة الميكانيكية لجسم يسقط سقوطاً حراً عند إهمال مقاومة الهواء:
أ- متزايدة.
ب- متناقصة.
ج- ثابتة.
د- صفراً.
9- عندما تؤثر قوة في جسم عمودياً على اتجاه إزاحته؛ فإن شغلها يكون:
أ- موجباً.
ب- سالباً.
ج- صفراً.
د- موجباً أو سالباً.
10- إذا كان شغل قوة مؤثرة في جسم بين موقعين، يعتمد على موقعه النهائي وموقعه الابتدائي، ولا يعتمد على المسار الفعلي للحركة؛ فإن هذه القوة توصف بأنها قوّة:
أ- احتكاك.
ب- محافظة.
ج- غير محافظة.
د- شدّ.
11- يتحرك جسم أفقياً بسرعة ثابتة مقدارها (5 m/s) شرقاً، ويقطع إزاحة مقدارها (50 m). إن الشغل الكلي المبذول على الجسم خلال هذه الإزاحة يساوي:
أ- 250 J.
ب- الطاقة الحركية له.
ج- صفراً.
د- طاقته الميكانيكية.
12- تتحرك سيارة بسرعة (15 m/s) شرقاً، بحيث كانت طاقتها الحركية (9 x 104 J). إذا تحركت السيارة غرباً بالسرعة نفسها؛ فإن مقدار طاقتها الحركية يساوي:
أ- 9 x 104 J.
ب- 9 x 104 J.
ج- 18 x 104 J.
د- 0 J.
13- يركض محمد بسرعة مقدارها (3 m/s). إذا تضاعف مقدار سرعته مرتين؛ فإن طاقته الحركية:
أ- تتضاعف مرتين.
ب- تتضاعف 4 مرات.
ج- تقل بمقدار النصف.
د- تقل بمقدار الربع.
14- تتحرك سيارة بسرعة (200 N) ويسير بسرعة ثابتة إزاحة مقدارها (10 m). إن مقدار الشغل الذي يبذله عدنان على الصندوق خلال الإزاحة يساوي:
أ- 0 J
ب- 2 J
ج- 200 J
د- 2000 J.
15- إذا كان الشغل الكلي المبذول على جسم يساوي صفراً، فهذا يعني أنّ الجسم:
أ- ساكن أو متحرك بسرعة ثابتة.
ب- ساكن أو متحرك بتسارع ثابت.
ج- ساكن أو يتحرك إلى أسفل بتسارع.
د- ساكن أو يتحرك إلى أعلى بتسارع.
السؤال الثاني:
أفسر إذا كان يبذل شغل أم لا في الحالات الآتية:
أ- تحمل هند حقيبتها، وتصعد بها إلى شقتها في الطابق الثاني.
تبذل هند شغلاً موجباً على الحقيبة من خلال تأثيرها بقوة إلى أعلى في الحقيبة بعكس وزنها، كما تبذل هند شغلاً موجباً ضد قوة الجاذبية المؤثرة فيها. بينما تبذل قوة الجاذبية الجاذبية شغلاً سالباً على كلٍ من هند والحقيبة.
ب- يرفع ياسر حقيبة كتبه رأسياً إلى أعلى عن سطح الأرض.
يبذل ياسر شغلاً موجباً على الحقيبة من خلال تأثيره بقوة إلى أعلى في الحقيبة بعكس وزنها، بينما تبذل قوة الجاذبية شغلاً سالباً على الحقيبة.
ج- تسير سارة أفقياً وهي تحمل حقيبة كتبها بين يديها.
لا يبذل شغل على الحقيبة؛ لأن اتجاه قوة سارة (إلى أعلى) واتجاه قوة الجاذبية (إلى أسفل) المؤثرتين في الحقيبة متعامدتان مع اتجاه الإزاحة. تبذل كل من سارة وقوة الجاذبية شغلاً عند رفع سارة لرجلها عن سطح الأرض وعند إنزالها لها، بينما لا يُبذل شغل خلال الحركة الأفقية.
د- تحاول ليلى دفع الأريكة، ولا تستطيع تحريكها من مكانها.
لا تبذل ليلى شغلاً على الأريكة؛ لأنه لا يوجد إزاحة في اتجاه قوة دفع ليلى.
السؤال الثالث:
أوضح هل يمكن لطاقة الوضع الناشئة عن الجاذبية أن تكون سالبة.
نعم؛ لأن طاقة الوضع الناشئة عن الجاذبية تعتمد على اختيارنا لمستوى الإسناد، فعندما يكون الجسم أسفل مستوى الإسناد فإن طاقة الوضع بالنسبة لمستوى الإسناد تكون سالبة.
السؤال الرابع:
أصدر حكماً: في أثناء دراستي وزميلتي أسماء لمبرهنة (الشغل – الطاقة الحركية)، فقالت: "إن الشغل الكلي المبذول على جسم يساوي طاقته الحركية النهائية". أناقش صحة قول أسماء.
لا يكون الشغل الكلي المبذول على جسم مساوياً لطاقته الحركية النهائية دائماً، بل يساوي التغير في طاقته الحركية. والشغل الكلي المبذول على جسم يساوي طاقته الحركية النهائية فقط عندما يبدأ الجسم حركته من السكون.
السؤال الخامس:
أحلل: قذفت كرة رأسياً إلى أعلى من سطح الأرض. عند أي ارتفاع يكون مقدار سرعتها مساوياً نصف مقدار سرعتها الابتدائية؟ أفسر إجابتي.
أفترض أن هذا الارتفاع هو (y)، والطاقة الميكانيكية عند هذا الارتفاع (MEy) تساوي الطاقة الميكانيكية الابتدائية (MEi) وتساوي الطاقة الميكانيكية عند أقصى ارتفاع (MEf). وأقصى ارتفاع تصله الكرة (h).
السؤال السادس:
أفسر البيانات: أثرت قوة محصلة متغيرة في جسم كتلته (10 kg)، فحركته من السكون إزاحة مقدارها (15 m)، كما هو موضح في الشكل المجاور. أحسب مقدار ما يأتي:
أ- الشغل الذي بذلته القوة المحصلة خلال (5 m) الأولى من بداية حركة الجسم.
الشغل الذي بذلته القوة خلال (5 m) الأولى من بداية حركة الجسم يساوي المساحة A عددياً، ويساوي مساحة مثلث طول قاعدته (5 m)، وارتفاعه (3 m).
ب- سرعة الجسم في نهاية الإزاحة (10 m).
الشغل الكلي الذي بذلته القوة المحصلة خلال (10 m) الأولى من بداية حركة الجسم يساوي مجموع المساحتين (A) و (B) عددياً، ويساوي مساحة شبه المنحرف الذي يشكلانه. وبحسب مبرهنة (الشغل-الطاقة الحركية)، فإن الشغل الكلي المبذول على الجسم يساوي التغير في طاقته الحركية. وأفترض أن سرعة الجسم في نهاية الإزاحة (10 m) رمزها (VB).
ج- الشغل الذي بذلته القوة المحصلة خلال الإزاحة كاملة (الشغل الكلي).
الشغل الكلي الذي بذلته القوة المحصلة الخارجية المتغيرة على الجسم يساوي عددياً مجموع المساحات (A) و (B) و (C)، أو يمكن حساب مساحة شبه المنحرف كاملاً الذي تكونه هذه المساحات. مساحة شبه المنحرف تساوي نصف مجموع القاعدتين مضروباً في البعد العمودي بينهما.
السؤال السابع:
أستعمل الأرقام: سيارة كتلتها (8x102 kg) تصعد تلاً طوله (5x102 m) بسرعة ثابتة مقدارها (25 m/s)، وتؤثر فيها قوى احتكاك (5x102 N).
إذا كانت زاوية ميلان التل على الأفقي (150)؛ فأحسب مقدار ما يأتي:
أ- القوة التي يؤثر بها محرك السيارة.
رمز قوة محرك السيارة (F):
ب- قدرة المحرك اللازمة كي تصعد السيارة التلّ بهذه السرعة.
السؤال الثامن:
أستعمل الأرقام: يجر قارب سفينة بحبل يصنع زاوية (250) أسفل الأفقي بسرعة ثابتة إزاحة مقدارها (2x102 m) بقوة شد مقدارها (2x103 N). إذا كان الحبل مهمل الكتلة وغير قابل للاستطالة؛ فأحسب مقدار ما يأتي:
أ- الشغل الذي يبذله القارب على السفينة.
ب- الشغل الذي تبذله القوى المعيقة المؤثرة في السفينة.
باستخدام مبرهنة (الشغل-الطاقة الحركية):
السؤال التاسع:
أحلل: يريد موسى رفع صندوق كتلته (100 kg) إلى ارتفاع (1 m) عن سطح الأرض. فاستخدم مستوى مائلاً طوله (2 m) يميل عن الأفقي بزاوية (300)، ودفع الصندوق إلى أعلى المستوى المائل بقوة موازية للمستوى بسرعة ثابتة. إذا كان مقدار قوة الاحتكاك الحركي المؤثرة في الصندوق (100 N)؛ فأحسب مقدار ما يأتي:
أ- الشغل الذي بذلته قوة الاحتكاك على الصندوق.
ب- الشغل الذي بذله موسى على الصندوق.
يوجد قوى غير محافظة مؤثرة في الصندوق تبذل شغلاً عليه، إذن الطاقة الميكانيكية غير محفوظة. ودُفع الصندوق بقوة (F) موازية للمستوى المائل بسرعة ثابتة (لا يوجد تغير في الطاقة الحركية).
ج- الشغل الذي بذلته قوة الجاذبية على الصندوق.
السؤال العاشر:
أستعمل الأرقام: تسحب ناديا صندوقاً كتلته (50 kg) على سطح أفقي خشن بحبل يميل على الأفقي بزاوية (450) إزاحة مقدارها (15 m)، كما هو موضح في الشكل المجاور. إذا علمت أن مقدار قوة الشد في الحبل (200 N)، واكتسب الصندوق تسارعاً مقداره (0.3 m/s2)؛ فأحسب مقدار ما يأتي:
أ- الشغل الذي بذلته ناديا على الصندوق.
ب- التغير في الطاقة الحركية للصندوق.
أحسب سرعة الصندوق في نهاية الإزاحة:
ثم أحسب التغير في طاقته الحركية:
ج- الشغل الذي بذلته قوة الاحتكاك الحركي على الصندوق.
أستخدم مبرهنة (الشغل – الطاقة الحركية):
د- الشغل الكلي المبذول على الصندوق.
السؤال الحادي عشر:
أستنتج: مصعد كتلته مع حمولته (2 x 103 kg)، يُرفع بمحرك كهربائي من سطح الأرض إلى ارتفاع (60 m) عن سطحها بسرعة ثابتة مقدارها (1 m/s). وتؤثر فيه في أثناء حركته إلى أعلى قوة احتكاك حركي ثابتة مقدارها (2 x 103 N)، أحسب مقدار ما يأتي:
أ- الشغل الذي يبذله المحرك على المصعد.
ب- شغل قوّة الاحتكاك الحركي.
ج- قدرة المحرّك.
د- التغير في الطاقة الميكانيكية للمصعد.
السؤال الثاني عشر:
التفكير الناقد: يوضح الشكل المجاور أفعوانية كتلة عربتها (2 x 102 kg) تتحرك من السكون من تل ارتفاعه (60 m) (الموقع A ) إلى أسفل التل على مسار مهمل الاحتكاك، وتمرّ في أثناء ذلك بمسار دائري رأسي عند الموقع (B) على شكل حلقة نصف قطرها (20 m) وتكمل مسارها مارّة بالموقع (D). أستعين بالشكل المجاور لأحسب مقدار ما يأتي:
أ- سرعة عربة الأفعوانية عند الموقع (B).
الطاقة الميكانيكية للعربة محفوظة لعدم وجود قوى غير محافظة تبذل شغلاً عليها، لذا فإن:
ب- سرعة عربة الأفعوانية عند الموقع (C).
ج- الشغل الكلي المبذول على العربة في أثناء حركتها من الموقع (B) إلى الموقع (C).
القوة الوحيدة المؤثرة في العربة التي تبذل شغلاً عليها هي قوة الجاذبية، وهي قوة محافظة. ويكون شغلها المبذول على العربة مساوياً سالب التغير في طاقة وضع العربة الناشيء عن الجاذبية، ويساوي أيضاً التغير في طاقتها الحركية.
د- الطاقة الميكانيكية لعربة الإفعوانية عند الموقع (D).
الطاقة الميكانيكية للعربة محفوظة لعدم وجود قوى غير محافظة تبذل شغلاً عليها، لذا فإن:
السؤال الثالث عشر:
ينزلق طفل كتلته (40 kg) بدءاً من السكون من قمة منزلق مائي أملس طوله (1 x 102 m) وارتفاعه (30 m) عن سطح الأرض، أنظر إلى الشكل المجاور. أجيب عمّا يأتي:
أ- أحسب مقدار الطاقة الميكانيكية للطفل عند قمة المنزلق.
بالرمز إلى نهاية المنزلق بالرمز (B)، وطاقة الوضع عندها تساوي صفراً؛؛ لأنه عند مستوى الإسناد. ولا يوجد قوة احتكاك؛ فتكون الطاقة الميكانيكية محفوظة.
ب- أحسب مقدار الطاقة الحركية للطفل عند نهاية المنزلق.
ج- أحسب مقدار سرعة الطفل عند نهاية المنزلق.
د- أحسب مقدار شغل قوة الجاذبية المبذول على الطفل في أثناء انزلاقه من قمة المنزلق إلى أسفله.
هـ- أفسر: هل يؤثر طول المنزلق في سرعة الطفل عند نهايته؟ أفسّر إجابتي.
لا يؤثر طول المنزلق في سرعة الطفل عند نهايته؛ لأنه لا يوجد قوى غير محافظة تبذل شغلاً عليه، فتكون الطاقة الميكانيكية محفوظة، ولا تتغير طاقته الحركية عند وصوله نهاية المنزلق بتغير طول المنزلق.
إعداد : شبكة منهاجي التعليمية
05 / 07 / 2024
النقاشات