إجابات أسئلة كتاب التمارين
المتتاليات والمتسلسلات
أكتب كلًّا مما يأتي من دون استعمال رمز المجموع: أعتمد الشكل المجاور الذي يمثل نمطاً هندسياً، وأجيب عن الأسئلة الثلاثة الآتية تباعاً:
(1)
1 + + + 2 +
(2)
4 + 10 + 18 + 28 + 40 + 54 + 70 + 88 + 108
(3)
+ + +
أعتمد الشكل المجاور الذي يمثل نمطا هندسياً، وأجيب عن الأسئلة الثلاثة الآتية تباعًا:
(4) أكتب الحد العام للمتتالية التي تمثل عدد المربعات المظللة في كل شكل.
an = 4n
(5) أكتب باستعمال رمز المجموع متسلسلة يمثل مجموعها عدد المربعات المظللة في أول عشرين شكلًا من هذا النمط، ثم أجد مجموع المتسلسلة.
= 840
(6) إذا كان طول ضلع كل مربع مظلّل هو وحدة واحدة، فأجد الحد العام للمتتالية التي تمثل مساحة المربعات البيضاء وسط كل شكل.
an = (n – 1)2
أجد الحد العام لكل متتالية حسابية مما يأتي، ثم أجد الحد العشرين منها:
(7) a6 = -8, a15 = -62
an = -6n + 28 , a20 = -92
(8) a11 = 43, d = 5
an = 5n - 12 , a20 = 88
(9) 25, 26.5, 28, 29.5, …
an = 1.5n + 23.5 , a20 = 53.5
أجد المجاميع الجزئية لكل من المتسلسلات الحسابية الآتية:
(10) الحدود العشرة الأولى من مضاعفات العدد 6
S10 = (6 + 60) = 330
(11) أول 100 عدد فردي من مجموعة الأعداد الصحيحة الموجبة.
S100 = (2(1) + (100 – 1) x 2) = 10000
مسارح: مسرح في صفه الأول 10 مقاعد، وفي صفه الثاني 12 مقعدًا، وفي صفه الثالث 14 مقعدًا، وهكذا حتى الصف الأخير منه :
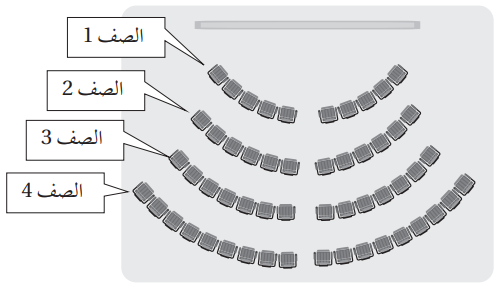
(12) أبين أنَّ عدد المقاعد في صفوف المسرح يشكل متتالية حسابية.
المتتالية حسابية أساسها 2
14 – 12 = 2 , 12 – 10 = 2
(13) أجد الحد العام للمتتالية الحسابية.
an = 2n + 8
(14) إذا كان في المسرح 14 صفًا من المقاعد، فكم مقعدًا في المسرح؟
S14 = (10 + 36) = 322
متسلسلة حسابية مجموع حدودها العشرين الأولى 730، ومجموع حدودها الثلاثين الأولى 1545:
(15) أجد الحد الأول من المتسلسلة.
S20 = 10(2a1 + 19d) = 730 2a1 + 19d = 73
S30 = 15(2a1 + 29d) = 1545 2a1 + 29d = 103
a1 = 8
(16) ما أساس المتسلسلة؟
d = 3
(17) أجد عدد حدود المتسلسلة التي تقل عن 101
an = 3n + 5
3n + 5 < 101 n < 32
n = 31
(18) متتالية حسابية، حدها العاشر ضعف حدّها الرابع، وحدها الثامن عشر 50، أجد الحد الأول من المتتالية، وأبرر إجابتي.
a10 = 2a4 a1 + 9d = 2(a1 + 3d)
a1 = 3d
a18 = 50 a1 + 17d = 50
3d + 17d = 50
d = 2.5
a1 = 7.5
متتالية حسابية، فيها الحدان المتتاليان x و y:
(19) أجد الحد التالي للحد y بدلالة x و y.
…, x, y, …
d = y – x
a = y + (y – x) = 2y - x
(20) إذا كان x يمثل الحد الثامن من المتتالية، فأجد الحد الأول بدلالة x و y.
a8 = a1 + 7(y – x) a1 = 8x – 7y
x = a1 + 7(y – x) a1 = 8x – 7y
إعداد : شبكة منهاجي التعليمية
06 / 09 / 2024
النقاشات