إجابات كتاب التمارين
التكامل بالتعويض
أجد كلاً من التكاملات الآتية:
(1)
(2)
(3)
(4)
(5)
(6)
أجد قيمة كل من التكاملات الآتية:
(7)
(8)
(9)
(10)
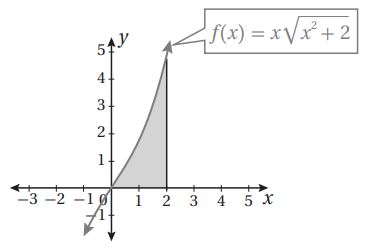 (11) أجد مساحة المنطقة المظللة في التمثيل البياني المجاور.
(11) أجد مساحة المنطقة المظللة في التمثيل البياني المجاور.
(12) الإيراد الحدي: يمثل الاقتران: الإيراد الحدي (بالدينار) لكل قطعة تباع من إنتاج إحدى الشركات، حيث عدد القطع المبيعة، و إيراد بيع قطعة بالدينار. أجد اقتران الإيراد ، علماً بأن .
يمثل الاقتران في كل مما يأتي ميل المماس لمنحنى الاقتران المار بالنقطة المعطاة، أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران :
(13)
(14)
(15) يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: ، حيث الزمن بالثواني، و سرعته المتجهة بالمتر لكل ثانية. إذا بدأ الجسيم حركته من نقطة الأصل، فأجد موقعه بعد ثانية من بدء الحركة.

