إجابات كتاب التمارين

إجابات كتاب التمارين

التكامل بالتعويض

أجد كلاً من التكاملات الآتية:

(1) $\int \frac{x}{\sqrt{x^{2} + 4}} d x$

$\begin{aligned} u = x^{2} + 4 \Rightarrow \frac{d u}{d x} = 2 x \Rightarrow d x = \frac{d u}{2 x} \\ \int \frac{x}{\sqrt{x^{2} + 4}} d x = \int \frac{x}{\sqrt{u}} \frac{d u}{2 x} = \int \frac{1}{2} u^{- \frac{1}{2}} d u = u^{\frac{1}{2}} + C = \sqrt{x^{2} + 4} + C \end{aligned}$

(2) $\int {(1 - \cos \frac{x}{2})}^{2} \sin \frac{x}{2} d x$

$\begin{aligned} u = 1 - c o s \frac{x}{2} \Rightarrow \frac{d u}{d x} = \frac{1}{2} s i n \frac{x}{2} \Rightarrow d x = \frac{2}{s i n \frac{x}{2}} d u \\ \int {(1 - c o s \frac{x}{2})}^{2} s i n \frac{x}{2} d x = \int u^{2} s i n \frac{x}{2} \frac{2}{s i n \frac{x}{2}} d u = \int 2 u^{2} d u = \frac{2}{3} u^{3} + C \\ = \frac{2}{3} {(1 - c o s \frac{x}{2})}^{3} + C \end{aligned}$

(3) $\int \csc^{5} x \cos^{3} x d x$

$\begin{aligned} \int c s c^{5} x c o s^{3} x d x = \int \frac{c o s^{3}}{s i n^{5} x} x d x = \int c o t^{3} x c s c^{2} x d x \\ \begin{aligned} u = c o t x \Rightarrow \frac{d u}{d x} & = - c s c^{2} x \Rightarrow d x = \frac{d u}{- c s c^{2} x} \\ \int c s c^{5} x c o s^{3} x d x & = \int c o t^{3} x c s c^{2} x d x \\ = \int u^{3} c s c^{2} \frac{d u}{- c s c^{2} x} = \int - u^{3} d u = - \frac{1}{4} u^{4} + C \end{aligned} \\ = - \frac{1}{4} c o t^{4} x + C \end{aligned}$

(4) $\int x \sin x^{2} d x$

$\begin{aligned} u = x^{2} \Rightarrow d x = \frac{d u}{2 x} \\ \int x s i n x^{2} d x = \int \frac{1}{2} s i n u d u = - \frac{1}{2} c o s u + C = - \frac{1}{2} c o s x^{2} + C \end{aligned}$

(5) $\int x^{3} (x + 2)^{7} d x$

$\begin{aligned} u = x + 2 \Rightarrow d x = d u, x = u - 2 \\ \begin{matrix} \int x^{3} (x + 2)^{7} d x = \int (u - 2)^{3} u^{7} d u = \int (u^{10} - 6 u^{9} + 12 u^{8} - 8 u^{7}) d u \\ = \frac{1}{11} u^{11} - \frac{3}{5} u^{10} + \frac{4}{3} u^{9} - u^{8} + C \\ = \frac{1}{11} (x + 2)^{11} - \frac{3}{5} (x + 2)^{10} + \frac{4}{3} (x + 2)^{9} - (x + 2)^{8} + C \end{matrix} \end{aligned}$

(6) $\int \frac{\ln \sqrt{x}}{x} d x$

$\begin{aligned} \int \frac{l n \sqrt{x}}{x} d x = \int \frac{\frac{1}{2} l n x}{x} d x \\ u = l n x \Rightarrow \frac{d u}{d x} = \frac{1}{x} \Rightarrow d x = x d u \\ \int \frac{l n \sqrt{x}}{x} d x = \int \frac{\frac{1}{2} l n x}{x} d x = \int \frac{1}{2} u d u = \frac{1}{4} u^{2} + C = \frac{1}{4} (l n x)^{2} + C \end{aligned}$

(7) $\int \frac{e^{\sqrt{x}}}{\sqrt{x}} d x$

$\begin{aligned} u = \sqrt{x} \Rightarrow \frac{d u}{d x} = \frac{1}{2 \sqrt{x}} \Rightarrow d x = 2 \sqrt{x} d u \\ \int \frac{e^{\sqrt{x}}}{\sqrt{x}} d x = \int \frac{e^{u}}{\sqrt{x}} \times 2 \sqrt{x} d u = 2 \int e^{u} d u = 2 e^{u} + C = 2 e^{\sqrt{x}} + C \end{aligned}$

(8) $\int \frac{\sin (\ln 4 x^{2})}{x} d x$

$\begin{aligned} \int \frac{s i n (l n 4 x^{2})}{x} d x = \int \frac{s i n (2 l n 2 x)}{x} d x \\ \begin{array}{r} u = 2 l n 2 x \Rightarrow \frac{d u}{d x} = \frac{2}{x} \Rightarrow d x = \frac{x}{2} d u \\ \int \frac{s i n (l n 4 x^{2})}{x} d x = \int \frac{s i n u}{x} \times \frac{x}{2} d u = \frac{1}{2} \int s i n u d u = - \frac{1}{2} c o s u + C \\ = - \frac{1}{2} c o s (2 l n 2 x) + C = - \frac{1}{2} c o s (l n 4 x^{2}) + C \end{array} \end{aligned}$

(9) $\int \sec^{2} x \cos^{3} (\tan x) d x$

$\begin{aligned} u = t a n x \Rightarrow \frac{d u}{d x} = s e c^{2} x \Rightarrow s e c^{2} x d x = d u \\ \int s e c^{2} x c o s^{3} (t a n x) d x = \int c o s^{3} u d u = \int c o s u c o s^{2} u d u \\ = \int c o s u (1 - s i n^{2} u) d u \\ v = s i n u \Rightarrow \frac{d v}{d x} = c o s u \Rightarrow c o s u d x = d v \\ \int c o s u (1 - s i n^{2} u) d u = \int (1 - v^{2}) d v = v - \frac{1}{3} v^{3} + C \\ = s i n u - \frac{1}{3} s i n^{3} u + C \\ = s i n (t a n x) - \frac{1}{3} s i n^{3} (t a n x) + C \end{aligned}$

ملحوظة: يمكن إيجاد هذا التكامل بإعادة كتابته على الصورة:

$\int s e c^{2} x c o s (t a n x) (1 - s i n^{2} (t a n x)) d x$

وبتعويض واحد فقط هو u = sin (tan x) .

أجد قيمة كل من التكاملات الآتية:

$\int_{6}^{20} \frac{8 x}{\sqrt{4 x + 1}} d x$ (10)

$\int_{2}^{5} \frac{1}{1 + \sqrt{x - 1}} d x$ (11)

$\int_{0}^{π / 2} \frac{\sin 2 x}{1 + \cos x} d x$ (12)

$\int_{1}^{4} \frac{(1 + \sqrt{x})^{3}}{\sqrt{x}} d x$ (13)

$\int_{0}^{π / 4} \frac{e^{\tan x}}{\cos^{2} x} d x$ (14)

$\int_{0}^{π / 3} \cos^{2} x \sin^{3} x d x$ (15)

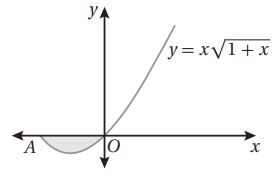(16) يبين الشكل المجاور جزءاً من منحنى الاقتران: $f (x) = x \sqrt{x + 1}$ .

أجد مساحة المنطقة المظللة في هذا الشكل.

في كل مما يأتي المشتقة الأولى للاقتران $f (x)$ ، ونقطة يمر بها منحنى $y = f (x)$ أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f (x)$ :

$f^{'} (x) = 16 \sin x \cos^{3} x; (\frac{π}{4}, 0)$ (17)

$f^{'} (x) = \frac{x}{\sqrt{x^{2} + 5}}; (2, 1)$ (18)

(19) يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: $v (t) = \frac{- 2 t}{{(1 + t^{2})}^{3 / 2}}$ ، حيث $t$ الزمن بالثواني، و $v$ سرعته المتجهة بالمتر لكل ثانية. إذا كان الموقع الابتدائي للجسيم هو $4 m$ ، فأجد موقع الجسيم بعد $t$ ثانية.