أتدرب وأحل المسائل
مشتقة اقترانات خاصة
أحدد قيم x للنقاط التي لا يكون عندها كلّ اقتران ممّا يأتي قابلاً للاشتقاق، مبرراً إجابتي:
(1) 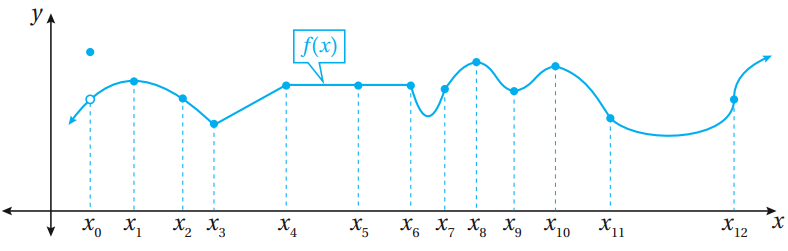
الاقتران f غير قابل للاشتقاق عندما x = x3, x = x4, x = x6 ؛ لأن لمنحناه رأس حاد أو زاوية عند هذه النقاط.
وهو غير قابل للاشتقاق عندما x = x0 ؛ لأنه غير متصل عندها،
وهو غير قابل للاشتقاق عندما x = x12 ؛ نظراً لوجود مماس رأسي عند هذه النقطة.
(2) 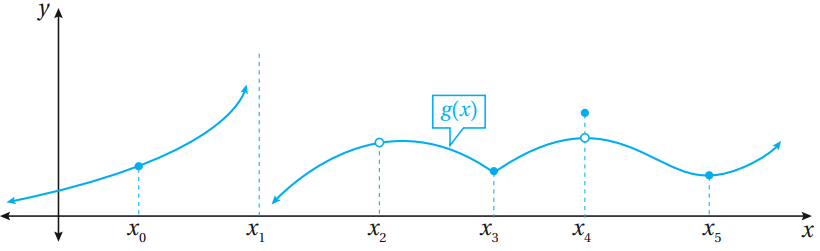
الاقتران g غير قابل للاشتقاق عندماx = x3 ؛ لأن لمنحناه زاوية عند هذه النقطة.
وهو غير قابل للاشتقاق عندما x = x0 ؛ لأنه غير متصل عندها،
وهو غير قابل للاشتقاق عندما x = x1, x = x2, x = x4 ؛ لأنه غير متصل عندها.
أجد مشتقة كل اقتران ممّا يأتي:
(3)
(4)
(5)
(6)
(7)
(8)
إذا كان: ، فأجيب عن السؤالين الآتيين تباعاً:
(9) أجد معادلة المماس لمنحنى الاقتران f عند النقطة ().
ميل المماس عند النقطة () :
معادلة المماس عند النقطة () :
(10) أجد معادلة العمودي على المماس لمنحنى الاقتران f عند النقطة ().
بما أن ميل المماس عند النقطة () هو ، فإن ميل العمودي على المماس هو:
معادلة العمودي على المماس هي:
(11) أجد قيمة x التي يكون عندها المماس أفقياً لمنحنى الاقتران:
(12) اختيار من متعدد: أي الآتية تمثل معادلة العمودي على المماس لمنحنى الاقتران: عندما x = π ؟
(a) y = -x + π - 1
(b) y = x - π - 1
(c) y = x - π + 1
(d) y = x + π + 1
عندما x = π ، فإن:
y = f (π) = sin π + cos π = -1
ميل المماس عند النقطة (π, -1) هو:
(π) = cos π - sin π = -1
بما أن ميل المماس هو -1 إذن ميل العمودي على المماس هو 1
معادلة العمودي على المماس:
y + 1 = 1 (x – π) → y = x – π - 1
الإجابة الصحيحة هي: b
(13) إذا كان: f(x) = ln (kx) ، حيث k عدد حقيقي موجب، و x > 0 ، فأبيّن أن .
إذا كان الاقتران: f(x) = ln (x) ، فأجيب عن السؤالين الآتيين تباعاً:
(14) أثبت أنّ مماس منحنى الاقتران عند النقطة (e, 1) يمر بنقطة الأصل.
ميل المماس عند النقطة (e, 1) هو:
معادلة المماس هي:
وهو مستقيم يمر بنقطة الأصل؛ لأن النقطة (0, 0) تحقق معادلته.
(15) أثبت أنّ المقطع x للعمودي على المماس لمنحى الاقتران عند النقطة (e, 1) هو
بما أن ميل المماس هو ، فإن ميل العمودي على المماس هو -e
معادلة العمودي على المماس:
y - 1 = -e (x – e) → y = -ex + e2 + 1
لإيجاد المقطع x لهذا المستقيم نضع y = 0 في معادلته:
يمثل الاقتران: موقع جسم يتحرك في مسار مستقيم، حيث s الموقع بالأمتار، و t الزمن بالثواني:
(16) أجد سرعة الجسم وتسارعه عندما t = 5 .
(17) أجد قيم t التي يكون عندها الجسم في حالة سكون لحظي.
(18) في أي اتجاه يتحرك الجسم عندما t = 4 .
بما أن إشارة السرعة المتجهة موجبة، فإن الجسم يتحرك لليمين عندما t = 4 .
(19) متى يعود الجسم إلى موقعه الابتدائي؟
موقع الابتدائي للجسم: s(0) = 0 m
العبارة التربيعية t2 – 4t + 5 مميزها سالب، وبالتالي لا تساوي صفراً.
إذن لا يعود الجسم إلى موقعه الابتدائي أبداً.
يمثل الاقتران: موقع جُسيم يتحرك في مسار مستقيم، حيث s الموقع بالأمتار، و t الزمن بالثواني:
(20) أحدد الموقع الابتدائي للجسيم.
(21) أجد تسارع الجسيم عندما تكون سرعته صفراً.
زنبرك: يتحرك جسم معلق بزنبرك إلى الأعلى وإلى الأسفل، ويحدد الاقتران: s(t) = 4 cos t موقع الجسم عند أي زمن لاحق، حيث t الزمن بالثواني، و s الموقع بالأمتار:
(22) أجد اقتراناً يمثل سرعة الجسم، واقتراناً آخر يمثل تسارعه عند أي لحظة.
(23) أجد سرعة الجسم وتسارعه عندما t = .
(24) أصف حركة الجسم.
من خصائص اقتران s(t) = 4 cos t نعرف أن الجسم يتحرك بمرور الزمن صعوداً وهبوطاً بين الموقعين s = 4 m , s = -4m وأنه يمر بنقطة الاتزان s = 0 أثناء هذه الحركة عندما t = حيث n أي عدد فردي موجب.
تتغير سرعة الجسم بمرور الزمن ونعرف من خصائص الاقتران v(t) = -4 sin t أن قيم السرعة تتراوح بين 4 m/s , -4 m/s ونلاحظ أن الجسم يصل إلى هذه السرعة عند اللحظات التي يمر فيها بنقطة الاتزان.
نلاحظ أن قيمة تسارع الجسم عند كل لحظة تساوي معكوس قيمة اقتران الموقع عند تلك اللحظة، وأن التسارع ينعدم عند مرور الجسم بنقطة الاتزان حيث تكون محصلة القوى المؤثرة في الجسم صفراً.
إعداد : شبكة منهاجي التعليمية
30 / 08 / 2024
النقاشات