أتدرب وأحل المسائل
الاقترانات اللوغاريتمية

أكتب كل معادلة لوغاريتمية ممّا يأتي في صورة أسيّة:
(1) log7 343 = 3
73 = 343
(2) log4 256 = 4
44 = 256
(3) log125 5 =
= 5
(4) log36 6 = 0.5
360.5 = 6
(5) log9 1 = 0
90 = 1
(6) log57 57 = 1
571 = 57
أكتب كل معادلة أسيّة ممّا يأتي في صورة لوغاريتمية:
(7) 26 = 64
log2 64 = 6
(8) 4-3 =
log4 = -3
(9) 63 = 216
log6 216 = 3
(10) 5-3 = 0.008
log5 0.008 = -3
(11) (51)1 = 51
log51 51 = 1
(12) 90 = 1
log9 1 = 0
أجد قيمة كل ممّا يأتي من دون استعمال الآلة الحاسبة:
(13) log3 81
log3 81 = log3 34 = 4
(14) log25 5
log25 5 = y
25y = 5
52y = 51
2y = 1
y =
إذن: log25 5 =
(15) log2 32
log2 32 = log2 25 = 5
إذن: log2 32 = 5
(16) log49 343
log49 343 = y
49y = 343
72y = 73
2y = 3
y =
إذن:log49 343 =
(17) log10 0.001
log10 0.001 = log10 10-3 = -3
(18) log 1
log 1 = 0
(19) log 4
log 4 = y
()y = 4
4-y = 41
-y = 1
y = -1
إذن:log 4 = -1
(20)
=
(21) log2
log2 = log2 = log2 = log2 = -
(22) loga
loga = loga =
(23) log10 (1 x 10-9)
log10 (1 x 10-9) = log10 10-9 = -9
(24) 8log
8log = 5
أمثل كل اقتران مما يأتي بيانياً، ثم أحدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبيناً إذا كان متناقصاً أم متزايداً:
(25) f(x) = log5 x
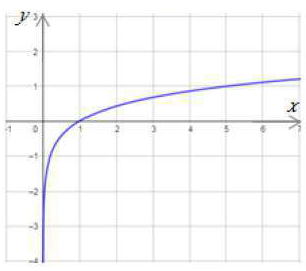
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متزايد.
(26) g(x) = log4 x
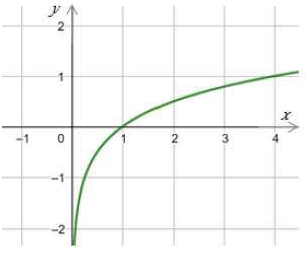
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متزايد.
(27) h(x) = log x
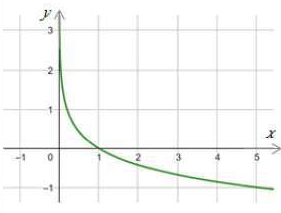
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متناقص.
(28) r(x) = log x
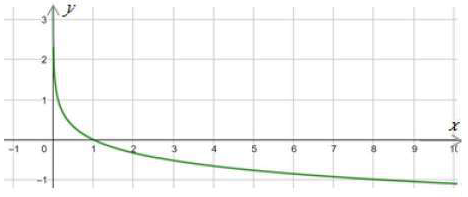
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متناقص.
(29) f(x) = log10 x
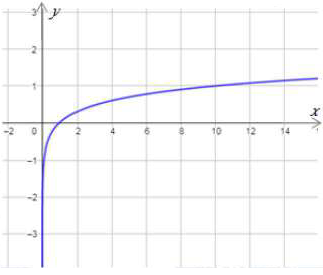
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متزايد.
(30) g(x) = log6 x
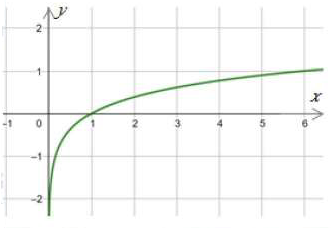
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحور y
الاقتران متزايد.
أجد مجال كل اقتران لوغاريتمي مما يأتي:
(31) f(x) = log3 (x – 2)
x – 2 > 0
x > 2
مجال هذا الاقتران هو (2 , ).
(32) f(x) = 5 – 2 log7 (x + 1)
x + 1 > 0
x > -1
مجال هذا الاقتران هو (-1 , ).
(33) f(x) = -3 log4 (-x)
-x > 0
x < 0
مجال هذا الاقتران هو ( , 0).
(34) أجد قيمة a التي تجعل منحنى الاقتران: f(x) = loga x يمر بالنقطة (32, 5).
f(x) = loga x
f(32) = loga 32
5 = loga 32
a5 = 32
a5 = (2)5
a = 2
(35) أجد قيمة c التي تجعل منحنى الاقتران: f(x) = logc x يمر بالنقطة ( , -4).
f(x) = logc x
f() = logc
-4 = logc
c-4 =
=
c4 = 4 → c2 = 2 → c =
لأن أساس اللوغاريتم لا يكون سالباً فإن: c =
 إعلانات: يمثل الاقتران: P(a) = 10 + 20 log5 (a + 1) مبيعات شركة (بآلاف الدنانير) من منتج جديد، حيث a المبلغ (بمئات الدنانير) الذي تنفقه الشركة على إعلانات المنتج. وتعني القيمة: P(1) ≈ 19 أن إنفاق JD 100 على الإعلانات يحقق إيرادات قيمتها JD 19000 من بيع المنتج:
إعلانات: يمثل الاقتران: P(a) = 10 + 20 log5 (a + 1) مبيعات شركة (بآلاف الدنانير) من منتج جديد، حيث a المبلغ (بمئات الدنانير) الذي تنفقه الشركة على إعلانات المنتج. وتعني القيمة: P(1) ≈ 19 أن إنفاق JD 100 على الإعلانات يحقق إيرادات قيمتها JD 19000 من بيع المنتج:
(36) أجد P(4) ، و P(24) ، و P(124) .
P(a) = 10 + 20 log5 (a + 1)
P(4) = 10 + 20 log5 (4 + 1)
P(4) = 10 + 20 log5 5
P(4) = 10 + 20(1) = 30
P(24) = 10 + 20 log5 (24 + 1)
P(24) = 10 + 20 log5 25
P(24) = 10 + 20 log5 52
P(24) = 10 + 20(2) = 50
P(124) = 10 + 20 log5 (124 + 1)
P(124) = 10 + 20 log5 125
P(124) = 10 + 20 log5 53
P(124) = 10 + 20(3) = 70
(37) أفسر معنى القيم التي أوجدتها في الفرع السابق.
القيمة P(4) = 30 تعني أن إنفاق JD400 على الإعلانات يحقق إيراداً قيمته JD30000 من بيع المنتج.
القيمة P(24) = 50 تعني أن إنفاق JD2400 على الإعلانات يحقق إيراداً قيمته JD50000 من بيع المنتج.
القيمة P(124) = 70 تعني أن إنفاق JD12400 على الإعلانات يحقق إيراداً قيمته JD70000 من بيع المنتج.
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات