إجابات كتاب التمارين
مشتقتا الضرب والقسمة والمشتقات العليا
أجد مشتقة كل اقتران ممّا يأتي:
(1) f(x) =
f ’(x) =
(2) f(x) = -cos x – sin x
f ’(x) = csc x cot x – cos x
(3) f(x) =
f (x) = , x ≠ 0
f ’(x) = = , x ≠ 0
(4) f(x) = x cos x
f ’(x) = -x csc2 x + cot x
(5) f(x) = 4x – x2 tan x
f ’(x) = 4 – x2 sec2 x – 2x tan x
(6) f(x) =
f ’(x) = =
(7) f(x) = x (1 - )
f (x) = x –
f ’(x) = 1 - = 1 -
(8) f(x) =
f ’(x) = =
(9) f(x) = (x + 1) ex
f ’(x) = (x + 1) ex + ex = (x + 2) ex
أجد معادلة المماس لكل اقتران ممّا يأتي عند النقطة المعطاة:
(10) f(x) = x2 cos x , ( , 0)
f ’(x) = -x2 sin x + 2x cos x
ميل المماس:
f ’() = -
معادلة المماس:
y - 0 = - (x - ) → y = - x +
(11) f(x) = , (π , -1)
f ’(x) = =
ميل المماس:
f ’(π) = = 1
معادلة المماس:
y +1 = 1(x - π) → y = x – π - 1
أجد إحداثيي النقطة (النقاط) التي يكون عندها لمنحنى كل اقتران ممّا يأتي مماس أفقي:
(12) f(x) =
f ’(x) = = = 0 → x = 1
النقطة المطلوبة هي:
(1, f(1)) = (1, 1)
(13) h(x) =
h’(x) = = = 0 → x = 0
النقطة المطلوبة هي:
(0, h(0)) = (0, 0)
(14) g(x) =
g’(x) = = = = 0 → x = 3
النقطة المطلوبة هي:
(3, g(3)) = (3,)
يبين الشكل المجاور منحنيي الاقترانين: f(x) ، و g(x) . إذا كان: u(x) = f(x)g(x) ، وكان: v(x) = ، فأجد كلاً ممّا يأتي:
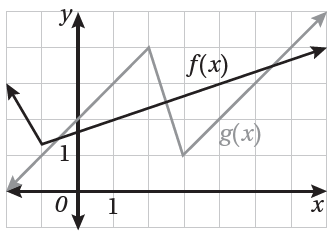
(15) u’(1)
u’(1) = f(1)g’(1) + g(1)f ’(1) = 2 x 1 + 3 x = 3
(16) v’(4)
v’(4) = = = -
(17) إذا كان: f(x) = x sec x ، فأثبت أنّ f ’(x) = sec x (1 + x tan x) .
f ’(x) = x sec x tan x + sec x = sec x (1 + x tan x)
(18) إذا كان: f(x) = ، حيث: x > 0 ، فأجد f ’(x) ، و f ’’(x) .
f ’(x) = = = -
f ’’(x) = - - =
يمثل الاقتران: v(t) = , t 0 السرعة المتجهة لسيّارة بدأت الحركة في مسار مستقيم، حيث تقاس v بالقدم لكل ثانية:
(19) أجد تسارع السيّارة عندما t = 5 .
a(t) =
a(5) = = -0.032 ft/s2
(20) أجد تسارع السيّارة عندما t = 20 .
a(20) = ≈ -0.007 ft/s2
(21) يعطى طول مستطيل بالمقدار 6t + 5 ، ويعطى عرضه بالمقدار ، حيث t الزمن بالثواني، والأبعاد بالسنتمترات. أجد معدل تغيّر مساحة المستطيل بالنسبة إلى الزمن.
A = (6t + 5) = 6 + 5
= 9 + = 9 + cm2/s
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات