أتحقق من فهمي
المتجهات في الفضاء
نظام الأحداثيات ثلاثي الأبعاد
أتحقق من فهمي صفحة (111):
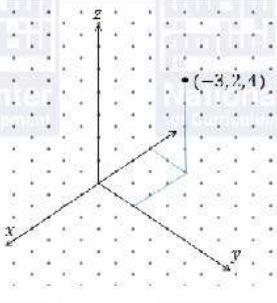
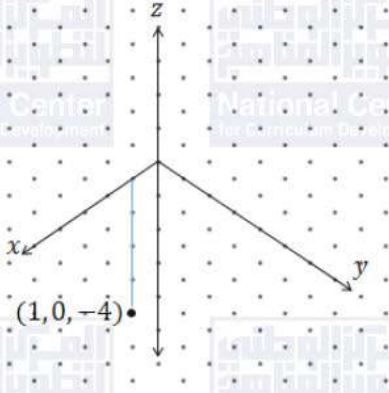
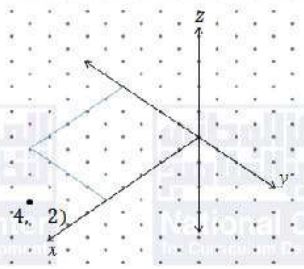
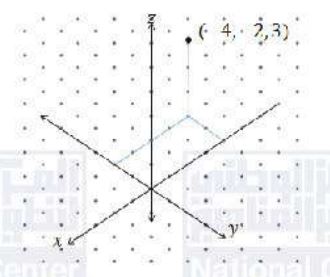
أعين كلاً من النقاط الآتية في نظام الأحداثيات ثلاثي الأبعاد:
(a)
(b)
(c)
(d)
المسافة بين نقطتين، وإحداثيات نقطة المنتصف في الفضاء
أتحقق من فهمي صفحة (113):
إذا كانت: ، فأجد كلاً مما يأتي:
(a) المسافة بين N وM.
(b) إحداثيات نقطة منتصف .
لتكن K منتصف القطعة المستقيمة ، فتكون:
مقدار المتجه في الفضاء
أتحقق من فهمي صفحة (114):
إذا كان: ، فأكتب المتجه بالصورة الإحداثية، ثم أجد مقداره.
جمع المتجهات وطرحها وضربها في عدد حقيقي هندسياً
أتحقق من فهمي صفحة (116):
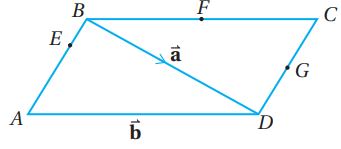 في متوازي الأضلاع ABCD المجاور، إذا كانت F نقطة منتصف ، وG نقطة منتصف ، وكانت: ، وكانت: ، وكانت: ، فاكتب كلاً مما يأتي بدلالة و:
في متوازي الأضلاع ABCD المجاور، إذا كانت F نقطة منتصف ، وG نقطة منتصف ، وكانت: ، وكانت: ، وكانت: ، فاكتب كلاً مما يأتي بدلالة و:
(a)
(b)
(c)
وذلك لأن كون الشكل متوازي الأضلاع
جمع المتجهات وطرحها وضربها في عدد حقيقي جبرياً
أتحقق من فهمي صفحة (117):
إذا كان: ، فأجد كلاً مما يأتي:
(a)
(b)
تساوي المتجهات
أتحقق من فهمي صفحة (117):
إذا كان: ، وكان: ، فأجد قيمة كل من .
متجها الموقع والإزاحة
أتحقق من فهمي صفحة (119):
إذا كانت: نقاطاً في الفضاء، فأجد كلاً مما يأتي:
(a) متجه موقع كل من النقاط: A وB وC.
(b) متجه الإزاحة من النقطة B إلى النقطة C.
(c) المسافة بين النقطة A والنقطة C.
كتابة المتجه بدلالة متجهات الوحدة الأساسية
أتحقق من فهمي صفحة (121):
اكتب كلاً من المتجهات الآتية بدلالة متجهات الوحدة الأساسية:
(a)
(b)
(c)
إيجاد متجه وحدة في اتجاه أي متجه
أتحقق من فهمي صفحة (122):
أجد متجه وحدة في اتجاه كل متجه مما يأتي:
(a)
وهذا متجه وحدة في
(b)
وهذا متجه وحدة في
(c)
ليكن متجه وحدة في اتجاه ، فيكون:





النقاشات