أتدرب وأحل المسائل

قاعدة السلسلة الأسئلة (25 - 41)

بكتيريا: يمثل الاقتران: A(t) = Ne^0.1t عدد الخلايا البكتيرية بعد t ساعة في مجتمع بكتيري:

(25) أجد معدل نمو المجتمع بعد 3 ساعات بدلالة الثابت N .

$\begin{array}{rl}& A\left(t\right)=N{e}^{0.1t}\\ & A^{\mathrm{\prime }}\left(t\right)=0.1N{e}^{0.1t}\\ & A^{\mathrm{\prime }}\left(3\right)=0.1N{e}^{0.3}\end{array}$

(26) إذا كان معدل نمو المجتمع بعد k ساعات هو 0.2 خلية لكل ساعة، فما قيمة k بدلالة الثابت N .

$\begin{array}{rl}& A^{\mathrm{\prime }}\left(k\right)=0.1N{e}^{0.1k}\\ & 0.2=0.1N{e}^{0.1k}\\ & e^{0.1k}=\frac{0.2}{0.1N}=\frac{2}{N}\\ & 0.1k=ln\frac{2}{N}\to k=10ln\frac{2}{N}\end{array}$

أجد المشتقة العليا المطلوبة في كلّ ممّا يأتي:

(27) $f\left(x\right)=\sin \pi x, f^{\prime \prime \mathrm{\prime }}\left(x\right)$

$\begin{array}{rl}& f\left(x\right)=sin\pi x\\ & f^{\mathrm{\prime }}\left(x\right)=\pi cos\pi x\\ & f^{\prime \prime }\left(x\right)=-{\pi }^{2}sin\pi x\\ & f^{\prime \prime \mathrm{\prime }}\left(x\right)=-{\pi }^{3}cos\pi x\end{array}$

(28) $f\left(x\right)=\cos (2x+1), f^{\left(5\right)}\left(x\right)$

$\begin{array}{rl}& f\left(x\right)=cos(2x+1)\\ & f^{\mathrm{\prime }}\left(x\right)=-2sin(2x+1)\\ & f^{\prime \prime }\left(x\right)=-4cos(2x+1)\\ & f^{\prime \prime \mathrm{\prime }}\left(x\right)=8sin(2x+1)\\ & f^{\left(4\right)}\left(x\right)=16cos(2x+1)\\ & f^{\left(5\right)}\left(x\right)=-32sin(2x+1)\end{array}$

(29) $f\left(x\right)=\cos x^2,f^{\prime \prime }\left(x\right)$

$\begin{array}{rl}& f\left(x\right)=cos x^2\\ & f^{\mathrm{\prime }}\left(x\right)=-2xsin x^2\\ & f^{\prime \prime }\left(x\right)=(-2x)(2xcos x^2)+(sin x^2)(-2)\\ & =-4x^{2}cos x^2-2sin x^2\end{array}$

(30) إذا كان الاقتران: y = e^{sin x} ، فأجد ميل مماس منحنى الاقتران عند النقطة (0, 1).

$\begin{array}{rl}& y=e^{sinx}\\ & \frac{dy}{dx}=e^{sinx}cos x\end{array}$

ميل المماس هو:

$m={\frac{dy}{dx}|}_{x=0}=e^{sin0}cos0=1$

(31) مواد مشعّة: يمكن نمذجة الكمية A (بالغرام) المتبقية من عينة كتلتها الابتدائية 20 g من عنصر البلوتونيوم بعد t يوماً باستعمال الاقتران: $A\left(t\right)=20{\left(\frac{1}{2}\right)}^{t/140}$ . أجد معدل تحلل عنصر البلوتويوم عند t = 2 .

$\begin{array}{rl}& A\left(t\right)=20{\left(\frac{1}{2}\right)}^{\frac{t}{140}}\\ & A^{\mathrm{\prime }}\left(t\right)=\frac{20}{140}(ln\frac{1}{2}){\left(\frac{1}{2}\right)}^{\frac{t}{140}}\\ & A^{\mathrm{\prime }}\left(2\right)=\frac{20}{140}(ln\frac{1}{2}){\left(\frac{1}{2}\right)}^{\frac{2}{140}}\approx -0.098\end{array}$

إذن يتحلل البلوتونيوم بمعدل 0.098 g كلّ يوم عندما t = 2 .

زنبرك: تتحرك كرة معلقة بزنبرك إلى الأعلى وإلى الأسفل، ويحدد الاقتران: s(t) = 0.1 sin 2.4t موقع الكرة عند أيّ زمن لاحق، حيث t الزمن بالثواني، و s الموقع بالسنتيمترات.

(32) أجد السرعة المتجهة للكرة عندما t = 1 .

$\begin{array}{rl}& s\left(t\right)=0.1sin2.4t\\ & v\left(t\right)=2.4\times 0.1cos2.4t=0.24cos2.4t\\ & v\left(1\right)=0.24cos2.4\approx -0.177\mathrm{cm}/\mathrm{s}\end{array}$

(33) أجد موقع الكرة عندما تكون سرعتها صفراً.

$\begin{array}{rl}v\left(t\right)=0& \to 0.24cos2.4t=0\\ & \to cos2.4t=0\end{array}$

وهذا يعني أنّ:

$|sin 2.4t|=1$

أي أنّ:

$sin 2.4t=1, \text{or }-1$

لكن موقع الكرة هو: 

$s\left(t\right)=0.1sin 2.4t$

وبتعويض قيمة sin 2.4t نجد أن الموقع هو:

$s=0.1\left(1\right)=0.1\text{or },s=0.1(-1)=-0.1$

إذن، عندما تكون سرعة الكرة صفراً يكون موقعها عند 0.1 cm أو -0.1 cm

(34) أجد موقع الكرة عندما تكون تسارعها صفراً.

$\begin{array}{rl}& a\left(t\right)=-0.24\times 2.4sin 2.4t=-0.576sin 2.4t\\ & a\left(t\right)=0\to sin 2.4t=0\end{array}$

لكن موقع الكرة هو: 

   $s\left(t\right)=0.1sin 2.4t$

وبتعويض قيمة sin 2.4t نجد أن الموقع هو: s = 0.1(0) = 0

إذن، عندما تكون تسارع الكرة صفراً يكون موقعها عند s = 0 ، أي عند مرورها بموقع الاتزان.

أجد معادلة المماس لمنحى كل معادلة وسيطية مما يأتي عند النقطة المحددة بقيمة t المعطاة:

(35) x = t + 2 , y = t² – 1 , t = 1

$\begin{array}{rl}& \frac{dy}{dt}=2t,\frac{dx}{dt}=1\\ & \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{2t}{1}=2t\end{array}$

ميل المماس:

$m={\frac{dy}{dx}|}_{t=1}=2\times 1=2$

نقطة التماس:

$x=1+2=3, y=(1{)}^2-1=0$

معادلة المماس:

$y-0=2(x-3)\to y=2x-6$

(36) $x=\frac{t}{2}, y=t^2-4, t=-1$

$\begin{array}{rl}& \frac{dy}{dt}=2t,\frac{dx}{dt}=\frac{1}{2}\\ & \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{2t}{\frac{1}{2}}=4t\end{array}$

ميل المماس:

$m={\frac{dy}{dx}|}_{t=-1}=4\times -1=-4$

نقطة التماس:

$x=-\frac{1}{2}, y=(-1{)}^2-4=-3$

معادلة المماس:

$y+3=-4(x+\frac{1}{2})\to y=-4x-5$

(37) $x=t-\sin t, y=1-\cos t, t=\frac{\pi }{3}$

$\begin{array}{rl}& \frac{dy}{dt}=sin t,\frac{dx}{dt}=1-cos t\\ & \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{sin t}{1-cos t}\end{array}$

ميل المماس:

$m={\frac{dy}{dx}|}_{t=\frac{\pi }{3}}=\frac{\sin \frac{\pi }{3}}{1-\cos \frac{\pi }{3}}=\frac{\frac{\sqrt{3}}{2}}{1-\frac{1}{2}}=\sqrt{3}$

نقطة التماس:

$x=\frac{\pi }{3}-\frac{\sqrt{3}}{2}, y=1-\frac{1}{2}=\frac{1}{2}$

معادلة المماس:

$y-\frac{1}{2}=\sqrt{3}(x-\frac{\pi }{3}+\frac{\sqrt{3}}{2})\to y=\sqrt{3}x-\frac{\sqrt{3}\pi }{3}+2$

(38) $x={\sec }^2 t-1, y=\tan t, t=-\frac{\pi }{4}$

$\begin{array}{rl}& \frac{dy}{dt}=se{c}^2 t,\frac{dx}{dt}=2\times sec t\times sec t tan t=2se{c}^2 t tan t\\ & \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{se{c}^2 t}{2se{c}^2 t tan t}=\frac{1}{2}cot t\end{array}$

ميل المماس:

$m={\frac{dy}{dx}|}_{t=-\frac{\pi }{4}}=\frac{1}{2}\cot (-\frac{\pi }{4})=-\frac{1}{2}$

نقطة التماس:

$x=se{c}^2 (-\frac{\pi }{4})-1=1, y=tan (-\frac{\pi }{4})=-1$

معادلة المماس:

$y+1=-\frac{1}{2}(x-1)\to y=-\frac{1}{2}x-\frac{1}{2}$

(39) يعطى منحنى بالمعادلة الوسيطية: $x=2(t-\sin t), y=2(1-\cos t)$ ، حيث: $0\le t\le 2\pi$ . أثبت أن ميل المماس وميل العمودي على المماس لمنحى هذه العلاقة عندما $t=\frac{\pi }{4}$ هما: $1-\sqrt{2}g\cdot 1+\sqrt{2}$ على الترتيب.

$\begin{array}{rl}& \frac{dy}{dt}=2\sin t,\frac{dx}{dt}=2(1-\cos t)\\ & \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{2\sin t}{2(1-\cos t)}=\frac{\sin t}{1-\cos t}\end{array}$

ميل المماس:

$\begin{array}{rl}m={\frac{dy}{dx}|}_{t=\frac{\pi }{4}}& =\frac{\sin \frac{\pi }{4}}{1-\cos \frac{\pi }{4}}=\frac{\frac{1}{\sqrt{2}}}{1-\frac{1}{\sqrt{2}}}=\frac{1}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1}\\ & =\sqrt{2}+1\end{array}$

ميل العمودي على المماس:

$m=\frac{-1}{\sqrt{2}+1}\times \frac{\sqrt{2}-1}{\sqrt{2}-1}=1-\sqrt{2}$

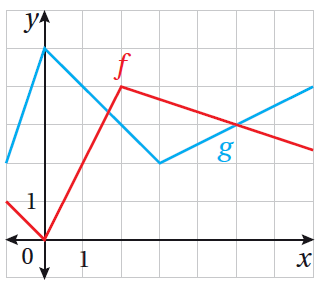
يبين الشكل المجاور منحنيي الاقترانين f(x) و g(x) . إذا كان:

h(x) = f(g(x)) ، وكان: p(x) = g(f(x)) ، فأجد كلاً مما يأتي:

(40) h' (1)

$h^{\mathrm{\prime }}\left(1\right)=f^{\mathrm{\prime }}\left(g\right(1\left)\right)\times g^{\mathrm{\prime }}\left(1\right)=f^{\mathrm{\prime }}\left(4\right)\times g^{\mathrm{\prime }}\left(1\right)$

g' (1) ميل المستقيم الذي يمر بالنقطتين (3, 2) و (0, 5) ويساوي -1

f ' (4) ميل المستقيم الذي يمر بالنقطتين (5, 3) و (2, 4) ويساوي -$\frac{1}{3}$

$h^{\mathrm{\prime }}\left(1\right)=-\frac{1}{3}\times -1=\frac{1}{3}$

(41) p' (1)

$p^{\mathrm{\prime }}\left(1\right)=g^{\mathrm{\prime }}\left(f\right(1\left)\right)\times f^{\mathrm{\prime }}\left(1\right)=g^{\mathrm{\prime }}\left(2\right)\times f^{\mathrm{\prime }}\left(1\right)$

g' (2) ميل المستقيم الذي يمر بالنقطتين (3, 2) و (0, 5) ويساوي -1

f ' (1) ميل المستقيم الذي يمر بالنقطتين (0, 0) و (2, 4) ويساوي 2

$p^{\mathrm{\prime }}\left(1\right)=-1\times 2=-2$